4. Torræð föll

Athugasemd

Nauðsynleg undirstaða

• Hornaföll, P7.

• Andhverfur falla. Sjá einnig undirstöðuatriði um andhverfur.

• Sjá einnig undirstöðuatriði um logra.

• Sjá einnig undirstöðuatriði um náttúrulega veldisvísisfallið og náttúrulega logrann.

We are stuck with technology when what we really want is just stuff that works.

- Douglas Adams, The Salmon of Doubt

---

4.1. Náttúrlegi logrinn

4.1.1. Skilgreining: Náttúrlegi logrinn

Skilgreining

Látum \(A_{x_0}\) tákna flatarmál svæðisins sem afmarkast af \(x\)-ás, grafinu \(y=\frac{1}{x}\) og línunum \(x=1\) og \(x=x_0\). Þá skilgreinum við náttúrlega logrann en: natural logarithm
Smelltu fyrir ítarlegri þýðingu. með formúlunni

\[\begin{split}\ln x_0 =\left\{\begin{array}{ll} A_{x_0} & \text{ef }x_0 \geq 1,\\ -A_{x_0} & \text{ef }0<x_0<1. \end{array} \right.\end{split}\]

Aðvörun

Fallið \(\ln\) er bara skilgreint fyrir jákvæðar rauntölur

4.1.2. Setning

Setning

Náttúrlegi logrinn er diffranlegur og afleiðan uppfyllir

\[\frac{d}{dx}\ln x=\frac{1}{x}.\]

Af þessu fylgir að logrinn er samfellt fall.

4.1.3. Setning

Setning

Fyrir allar tölur \(x,y>0\) gildir að:

1. \(\ln(1) = 0\)

2. \(\ln(xy)=\ln x+\ln y\)

3. \(\ln(1/x)=-\ln x\)

4. \(\ln(x/y)=\ln x-\ln y\)

5. \(\ln (x^r)=r\ln x\), fyrir \(r \in \mathbb Q\).

4.2. Veldisvísisfallið

4.2.1. Setning

Setning

Fallið \(\ln x\) er strangt vaxandi og þar með eintækt.

4.2.2. Skilgreining: Veldisvísisfallið

Skilgreining

Veldisvísisfallið en: exponential function
Smelltu fyrir ítarlegri þýðingu. , \(\exp x\), er skilgreint sem andhverfa fallsins \(\ln x\). Skilgreiningarsvæði \(\exp x\) er jafnt myndmengi \(\ln x\) sem er \({{\mathbb R}}\). Myndmengi \(\exp x\) er jafnt skilgreiningarsvæði \(\ln x\) sem er bilið \((0,\infty)\).

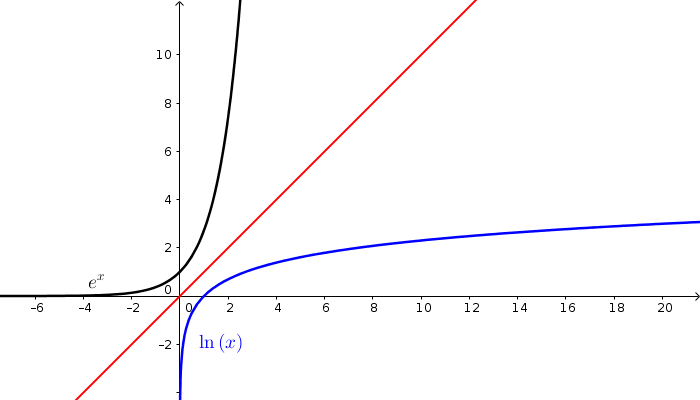
4.2.3. Skilgreining: Talan \(e\)

Skilgreining

Skilgreinum töluna með \(e=\exp 1\).

Það þýðir að \(\ln(e)=1\), og talan \(e\) ákvarðast þess vegna af því að flatarmál svæðisins milli \(x\)-ás og grafs \(\frac 1x\) á bilinu \([1,e]\) sé 1.

Athugasemd

Hver er munurinn á \(e^x\) og \(\exp(x)\) ?

\(e^x\) er aðeins skilgreint þegar \(x\) er ræð tala, en \(\exp(x)\) er skilgreint fyrir allar rauntölur því logrinn, \(\ln:(0,\infty)\to {{\mathbb R}}\), er átækur.

Það er hins vegar hægt að sýna að

\[\exp(x)=\lim_{r\to x, r\text{ ræð tala}} e^r.\]

Því er eðlilegt að rita fyrir rauntölu \(x\), hvort sem hún er ræð eða óræð, að \(e^x=\exp x\). Þannig að héðan í frá gerum við engan greinarmun á \(e^x\) og \(\exp x\), við notum bara það sem lítur betur út fagurfræðilega.

Athugasemd

Athugið að

\[e^{\ln x}=x \text{ fyrir allar tölur }x>0\qquad \text{og} \qquad \ln(e^x)=x \text{ fyrir allar tölur }x.\]

4.2.4. Eiginleikar veldisvísisfallsins

Út frá eiginleikum lograns fáum við svo eftirfarandi

1. \(e^0=1\),

2. \(e^{x+y}=e^x e^y\),

3. \(e^{-x}=\frac{1}{e^x}\),

4. \(e^{x-y}=\frac{e^x}{e^y}\),

5. \(\left(e^x\right)^y=e^{xy}\), fyrir \(y \in \mathbb Q\).

Athugasemd

Hænan eða eggið? Hér höfum við nálgast \(\ln\) og \(\exp\) þannig að við byrjum á að skilgreina \(\ln\) með heildi (flatarmáli) og finnum svo andhverfu lograns, \(\exp\).

Einnig væri mögulegt að byrja á því að sýna að \(e^x\) sé vel skilgreint, ekki bara fyrir ræð \(x\) heldur einnig óræð. Það myndum við gera með því að nota markgildið \(\exp(x)=\lim_{r\to x, r\text{ ræð tala}} e^r\) hér að ofan, og taka þá \(e^x\) sem skilgreiningu á \(\exp x\) og finna svo andhverfuna, \(\ln\).

Báðar þessar aðferðir hafa kosti og galla, en við notum þá fyrri vegna þess að hún gefur myndræna framsetningu á logranum.

4.3. Önnur veldisvísisföll og lograr

4.3.1. Skilgreining

Skilgreining

Fyrir tölu \(a>0\) og rauntölu \(x\) skilgreinum við

\[a^x=e^{x\ln a}.\]

4.3.2. Skilgreining

Skilgreining

Andhverfa fallsins \(a^x\) er kölluð logri með grunntölu \(a\) og táknuð með \(\log_a x\). Fallið \(\log_a x\) er skilgreint fyrir öll \(x>0\).

4.3.3. Athugasemd

Athugasemd

\[y =\log_a(x)\qquad \text{ þá og því aðeins að } \qquad x = a^y.\]

4.3.4. Reiknireglur

Setning

Fyrir rauntölu \(a>0\) og allar rauntölur \(x,y\) gildir að:

1. \(a^0=1\)

2. \(a^1=a\)

3. \(a^{x+y}=a^xa^y\)

4. \(a^{-x}=\frac{1}{a^x}\)

5. \(a^{x-y}=\frac{a^x}{a^y}\)

6. \(\big(a^x\big)^y=a^{xy}\)

7. \((ab)^x=a^xb^x\) (hér er forsenda að \(b>0\)).

Setning

Fyrir rauntölu \(a>0\) og allar rauntölur \(x,y\) gildir að:

1. \(\log_a 1=0\)

2. \(\log_a a = 1\)

3. \(\log_a(xy)=\log_a x+\log_a y\)

4. \(\log_a (1/x)=-\log_a x\)

5. \(\log_a (x/y)=\log_a x-\log_a y\)

6. \(\log_a (x^y)=y\log_a x\)

7. \(\log_a x=\frac{\log_b x}{\log_b a}\) (hér er forsenda að \(b>0\)).

4.4. Eiginleikar veldisvísisfalla og logra

4.4.1. Setning

Setning

1. \(\frac{d}{dx}\ln x=\frac 1x\)

2. \(\frac{d}{dx}e^x=e^x\)

3. \(\frac{d}{dx}a^x=(\ln a)a^x\)

4. \(\frac{d}{dx}\log_a x=\frac{1}{(\ln a)x}\)

4.4.2. Setning

Setning

Ef \(a>0\) þá er

1. \(\lim_{x\to \infty} \frac{x^a}{e^x} = 0\)

2. \(\lim_{x\to \infty} \frac{\ln(x)}{x^a} = 0\)

3. \(\lim_{x\to -\infty} |x|^a e^x = 0\)

4. \(\lim_{x\to 0^+} x^a\, \ln(x) = 0\)

Athugasemd

Athugið að setningin að ofan gildir óháð því hversu stórt \(a\) er (liðir 1 og 3) eða hversu lítið \(a\) er (liðir 2 og 4).

Með öðrum orðum:

• Veldisvísisföll vaxa hraðar en allar margliður.

• Lograr vaxa hægar en allar margliður.

4.4.3. Æfingadæmi

Æfingadæmi

Hakið við réttan kross.

1. \(\ln(\frac{6x^2}{e^x}) = \ln(6)+2\ln(x)-x\)

2. \(\ln(4a+6b) = 2\ln(2a)+\ln(6b)\)

3. \(\frac{\ln(x)}{\ln(y)} = \ln\left( \frac{\ln(x)}{\ln(y)} \right)\)

4. Fyrir öll \(x \in \mathbb{R}\) gildir að \(e^{\ln(x)} = 1\)

Lausn

Lograreglur gefa

\[\ln\left(\frac{6x^2}{e^x}\right) = \ln(6x^2) - \ln(e^x) = \ln(6) + 2\ln(x) + x.\]

4.5. Andhverfur hornafalla

4.5.1. Andhverfa sínus

Fallið \(\sin(x)\) skilgreint á öllum rauntalnaásnum er ekki eintækt og á sér því ekki andhverfu.

Við getum hins vegar takmarkað okkur við hálfa lotu, þ.e. skoðum bara \(x\in [-\frac \pi 2, \frac \pi 2]\). \(\sin(x)\) takmarkað við þetta bil táknum við með \({{\text{Sin}}}(x)\). \({{\text{Sin}}}\) er strangt vaxandi og því eintækt á þessu bili, og hefur þar af leiðandi andhverfu.

4.5.2. Skilgreining: arcsin

Skilgreining

Andhverfa sínussins, táknuð \(\arcsin(x)\) (eða \(\sin^{-1}(x)\)), er andhverfa \({{\text{Sin}}}\) og hefur því myndmengið \([-\frac \pi 2, \frac \pi 2]\) og skilgreiningarmengið \([-1,1]\).

4.5.3. Andhverfa kósínus

Fallið \(\cos(x)\) skilgreint á öllum rauntalnaásnum er ekki eintækt og á sér því ekki andhverfu.

Við getum hins vegar takmarkað okkur við hálfa lotu, þ.e. skoðum bara \(x\in [0, \pi]\). \(\cos(x)\) takmarkað við þetta bil táknum við með \({{\text{Cos}}}(x)\). \({{\text{Cos}}}\) er strangt minnkandi og því eintækt á þessu bili, og hefur þar af leiðandi andhverfu.

4.5.4. Skilgreining: arccos

Skilgreining

Andhverfa kósínussins, táknuð \(\arccos(x)\) (eða \(\cos^{-1}(x)\)), er andhverfa \({{\text{Cos}}}\) og hefur því myndmengið \([0,\pi]\) og skilgreiningarmengið \([-1,1]\).

4.5.5. Andhverfa tangens

Fallið \(\tan(x) = \frac{\sin(x)}{\cos(x)}\) skilgreint á \(\{x \in {{\mathbb R}}; x \neq \pi k + \frac \pi 2, k \in {{\mathbb Z}}\}\) er ekki eintækt og á sér því ekki andhverfu.

Við getum hins vegar takmarkað okkur við eina lotu, þ.e. skoðum bara \(x\in (-\frac \pi 2, \frac \pi 2)\). Athugið að hér eru endapunktar bilsins ekki með. \(\tan(x)\) takmarkað við þetta bil táknum við með \({{\text{Tan}}}(x)\). \({{\text{Tan}}}\) er strangt vaxandi og því eintækt á þessu bili, og hefur þar af leiðandi andhverfu.

4.5.6. Skilgreining: arctan

Skilgreining

Andhverfa tangensins, táknuð \(\arctan(x)\) (eða \(\tan^{-1}(x)\)), er andhverfa \({{\text{Tan}}}\) og hefur því myndmengið \((-\frac \pi 2, \frac \pi 2)\) og skilgreiningarmengið \((-\infty,\infty)\). Þar að auki þá er \(\lim_{x\to \infty} \arctan(x) = \frac \pi 2\) og \(\lim_{x\to -\infty} \arctan(x) = -\frac \pi 2\).

4.5.7. Setning

Setning

1. \(\frac d{dx} \arcsin(x) = \frac 1{\sqrt{1-x^2}}\)

2. \(\frac d{dx} \arccos(x) = \frac {-1}{\sqrt{1-x^2}}\)

3. \(\frac d{dx} \arctan(x) = \frac 1{1+x^2}\)

4.6. Breiðbogaföll

4.6.1. Skilgreining: cosh og sinh

Skilgreining

Við skilgreinum breiðbogasínus en: hyperbolic sine
Smelltu fyrir ítarlegri þýðingu. , \(\sinh\), og breiðbogakósínus en: hyperbolic cosine
Smelltu fyrir ítarlegri þýðingu. , \(\cosh\), með eftirfarandi formúlum

\[\begin{split}\begin{aligned} \sinh(x) &= \frac{e^x - e^{-x}}2,\\ \cosh(x) &= \frac{e^x + e^{-x}}2.\end{aligned}\end{split}\]

4.6.2. Setning

Setning

1. \(\frac d{dx} \sinh(x) = \cosh(x)\)

2. \(\frac d{dx} \cosh(x) = \sinh(x)\)

Aðvörun

Það er enginn mínus í afleiðu \(\cosh\) eins og í afleiðu \(\cos\).

4.6.3. Setning

Setning

1. \(\sinh(0) = 0\) og \(\cosh(0) = 1\)

2. \(\cosh^2(x) - \sinh^2(x) = 1\)

3. \(\sinh(-x) = -\sinh(x)\)

4. \(\cosh(-x) = \cosh(x)\)

5. \(\sinh(x+y) = \sinh(x)\cosh(y) + \cosh(x)\sinh(y)\)

6. \(\cosh(x+y) = \cosh(x)\cosh(y) + \sinh(x)\sinh(y)\)

7. \(\cosh(2x) = \cosh^2(x) + \sinh^2(x) = 1+2\sinh^2(x) = 2\cosh^2(x)-1\)

8. \(\sinh(2x) = 2\sinh(x)\cosh(x)\)

4.6.4. Skilgreining: tanh

Skilgreining

Við skilgreinum breiðbogatangens en: hyperbolic tangent
Smelltu fyrir ítarlegri þýðingu. með

\[\tanh(x) = \frac{\sinh(x)}{\cosh(x)}\]

4.6.5. Setning

Setning

1. \(\tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}\)

2. \(\frac d{dx} \tanh(x) = \frac{1}{\cosh^2(x)}\)

3. \(\lim_{x\to \infty} \tanh(x) = 1\)

4. \(\lim_{x\to -\infty} \tanh(x) = -1\)

4.7. Andhverfur breiðbogafalla

4.7.1. Andhverfa breiðbogasínussins og breiðbogatangensins

Af Setningum 4.6.2 (1) og 4.6.5 (2) sjáum við að afleiður \(\sinh\) og \(\tanh\) eru jákvæðar og föllin því stranglega vaxandi. Þau eru þar með eintæk og eiga sér andhverfur.

4.7.2. Skilgreining

Skilgreining

Andhverfa breiðbogasínussins en: area-hyperbolic sine, inverse hyperbolic sine
Smelltu fyrir ítarlegri þýðingu. , táknuð \({{\text{arsinh}}}(x)\) (eða \(\sinh^{-1}(x)\)), er andhverfa \(\sinh\) og hefur myndmengið \((-\infty,\infty)\) og skilgreiningarmengið \((-\infty,\infty)\). Þar að auki þá er

\[{{\text{arsinh}}}(x) = \ln\left(x+\sqrt{x^2+1}\right)\]

Andhverfa breiðbogatangensins en: inverse hyperbolic tangent
Smelltu fyrir ítarlegri þýðingu. , táknuð \({{\text{artanh}}}(x)\) (eða \(\tanh^{-1}(x)\)), er andhverfa \(\tanh\) og hefur myndmengið \((-\infty,\infty)\) og skilgreiningarmengið \((-1,1)\). Þar að auki þá er

\[{{\text{artanh}}}(x) = \frac 12 \ln\left(\frac{1+x}{1-x}\right)\]

4.7.3. Andhverfa breiðbogakósínussins

Þar sem \(\cosh\) er ekki eintækt fall þá verðum við að beita svipuðum aðferðum eins og þegar við fundum \(\arcsin\) til þess að finna andhverfu þess. Það er, við þurfum að takmarka skilgreiningarmengi þess.

Táknum \(\cosh(x)\) takmarkað við bilið \([0,\infty)\) með \({{\text{Cosh}}}(x)\). Fallið \({{\text{Cosh}}}\) er strangt vaxandi og því eintækt á þessu bili, og á sér þar með andhverfu.

4.7.4. Skilgreining

Skilgreining

Andhverfa breiðbogakósínussins en: inverse hyperbolic cosine
Smelltu fyrir ítarlegri þýðingu. , táknuð \({{\text{arcosh}}}(x)\) (eða \(\cosh^{-1}(x)\)), er andhverfa \({{\text{Cosh}}}\) og hefur því myndmengið \([0,\infty)\) og skilgreiningarmengið \([1,\infty)\). Þar að auki þá er

\[{{\text{arcosh}}}(x) = \ln\left(x+\sqrt{x^2-1}\right)\]

4.7.5. Í framtíðinni

Við höfum séð að veldisvísisfallið og logrinn tengjast breiðbogaföllunum töluvert og það sama á við um hornaföllin. Seinna, nánar tiltekið í Stærðfræðigreiningu III, þá sjáið þið að hornaföllin og breiðbogaföllin eru bara mismunandi hliðar á veldisvísisfallinu.