1. Tölur og föll

Athugasemd

Nauðsynleg undirstaða

• Undirstöðuatriði tölur og talnakerfi.

• Forgangsröðun aðgerða.

• Reiknireglur.

• Brotareikningur.

• Veldi og rætur.

• Sjá undirstöðuatriði um föll.

1.1. Inngangur

There is a theory which states that if ever anyone discovers exactly what the Universe is for and why it is here, it will instantly disappear and be replaced by something even more bizarre and inexplicable. There is another theory which states that this has already happened.

- Douglas Adams, The Restaurant at the End of the Universe

1.1.1. Grunnhugmyndin

Stærðfræðigreining grundvallast á því að mæla breytingu (oft með tilliti til tíma)

• Eðlisfræði: hraði, hröðun, massi, orka, vinna, afl, þrýstingur

• Rúmfræði: flatarmál, rúmmál, lengd, massamiðja

• Hagnýtingar: hagfræði, stofnstærðir, hámörkun/lágmörkun, hreyfikerfi, hitaflæði

• Stærðfræði: markgildi, hermun, jafnvægisástand

Sett fram samtímis, en óháð, af Isaac Newton og Gottfried Leibniz í lok 17. aldar.

1.1.2. Ítarefni

Fyrir nánari útlistun á hugtökunum sem við fjöllum um þá er hægt að skoða, auk kennslubókarinnar,

• http://edbook.hi.is/undirbuningur_stae

• http://stae.is/hugtakasafn

• http://stae.is/os, íslensk-ensk og ensk-íslensk orðaskrá

• http://planetmath.org

• http://mathworld.wolfram.com

• http://en.wikipedia.org (ath. enska útgáfan)

Einnig getur verið gagnlegt að kannast við grísku bókstafina:

1.1.3. Forrit

• GeoGebra http://www.geogebra.org

• WolframAlpha http://www.wolframalpha.com

• Matlab http://www.mathworks.com (sjá https://notendur.hi.is/~jonasson/matlab/)

• Octave http://www.gnu.org/software/octave/ (opið og ókeypis, svipað og Matlab)

• Sage http://www.sagemath.org/ (opið og ókeypis, byggt á Python)

• Mathematica http://www.wolfram.com/mathematica/

---

1.2. Tölur

1.2.1. Skilgreining: Tölur

Skilgreining

1. Náttúrlegu tölurnar en: natural number
   Smelltu fyrir ítarlegri þýðingu. eru tölurnar \(1, 2, 3, 4, \ldots\) og mengi þeirra er táknað með \(\mathbb{N}\).

2. Mengi heiltalna en: integer
   Smelltu fyrir ítarlegri þýðingu. er táknað með \(\mathbb{Z}\). \(\mathbb{Z}= \ldots,-2,-1,0,1,2,3,\ldots\)

3. Mengi ræðra talna en: rational number
   Smelltu fyrir ítarlegri þýðingu. er táknað með \(\mathbb{Q}\). \(\mathbb{Q}= \{ \frac pq ; p,q \in \mathbb{Z}, q\neq 0\}\).

4. Mengi rauntalna en: real number
   Smelltu fyrir ítarlegri þýðingu. er táknað með \(\mathbb{R}\).

5. Mengi tvinntalna en: complex number
   Smelltu fyrir ítarlegri þýðingu. er táknað með \(\mathbb{C}\).

Athugasemd

Margir vilja telja \(0\) með sem náttúrlega tölu. Það er eðlilegt ef maður lítur á náttúrlegu tölurnar þannig að þær tákni fjölda. Ef maður lítur hins vegar þannig á að þær séu notaðar til að númera hluti þá er 0 ekki með.

Sjá einnig http://edbook.hi.is/undirbuningur_stae/kafli01/index.html#talnakerfi.

1.2.2. Smíði rauntalna

Rauntölur eru smíðaðar úr ræðu tölunum með því að fylla upp í götin.

T.d. eru

\[\begin{split}\begin{aligned} \pi &= 3,1415926\ldots, \qquad \text{og}\\ \sqrt 2 -4 &= -2,58578\ldots\end{aligned}\end{split}\]

ekki ræðar tölur (það er ekki hægt að skrifa þær sem brot \(\frac ab\), þar sem \(a\) og \(b\) eru heilar tölur), en þær eru rauntölur. Slíkar tölur kallast óræðar en: irrational number
Smelltu fyrir ítarlegri þýðingu. .

Sjá einnig Óræðar tölur | stæ.is.

1.2.3. Frumsendan um efra mark

Látum \(A\) vera mengi af rauntölum sem er þannig að til er tala \(x\), þannig að fyrir allar tölur \(a \in A\) þá er

\[a\leq x.\]

Þá er til rauntala \(x_0\) sem kallast efra mark en: least upper bound, lowest upper bound, supremum
Smelltu fyrir ítarlegri þýðingu. fyrir \(A\), sem er þannig að \(a\leq x_0\) fyrir allar tölur \(a\in A\) og ef \(x<x_0\) þá er til tala \(a\in A\) þannig að \(a>x\).

Sjá einnig Least-upper-bound property.

1.3. Bil

1.3.1. Skilgreining: Bil

Skilgreining

Látum \(a\) og \(b\) vera rauntölur þannig að \(a<b\). Skilgreinum

1. opið bil \((a,b)=\{x\in \mathbb{R}; a<x<b\}\)

2. lokað bil \([a,b]=\{x\in \mathbb{R}; a\leq x\leq b\}\)

3. hálfopið bil \([a,b)=\{x\in \mathbb{R}; a\leq x<b\}\)

4. hálfopið bil \((a,b]=\{x\in \mathbb{R}; a< x\leq b\}\)

Þessi bil sem er skilgreind hér fyrir ofan eru kölluð endanleg. Til eru fleiri gerðir af bilum:

5. opið óendanlegt bil \((a,\infty)=\{x\in \mathbb{R}; a<x\}\)

6. opið óendanlegt bil \((-\infty, a)=\{x\in \mathbb{R}; x<a\}\)

7. lokað óendanlegt bil \([a,\infty)=\{x\in \mathbb{R}; a\leq x\}\)

8. lokað óendanlegt bil \((-\infty, a]=\{x\in \mathbb{R}; x\leq a\}\)

9. allur rauntalnaásinn \((-\infty, \infty)= \mathbb{R}\).

1.3.2. Skilgreining: Bil

Skilgreining

Mengi \(A\) af rauntölum kallast bil en: interval
Smelltu fyrir ítarlegri þýðingu. ef um allar tölur \(a<b\) sem eru í menginu \(A\) gildir að ef \(a<x<b\) þá er \(x\) líka í menginu \(A\). Þ.e. bil innihalda engin göt.

Athugasemd

Sérhvert bil á rauntalnaásnum er af einni þeirra gerða sem talin er upp í Skilgreining 1.3.1. Þessi staðhæfing er jafngild frumsendunni um efra mark.

Athugasemd

Það er jafngilt að segja

\[x \in (a-\eta,a+\eta)\]

og

\[|x-a| < \eta.\]

1.3.3. Æfingadæmi

Æfingadæmi

Hakið við réttan kross.

1. Talan 2,4 er náttúruleg tala.

2. Til eru tölur sem eru bæði í senn ræðar og óræðar.

3. Allar ræðar tölur eru rauntölur en ekki eru allar rauntölur ræðar.

4. Kvaðratrætur náttúrulegra talna eru allar óræðar.

Lausn

1. Talan 2,4 er ekki náttúruleg tala því hún er ekki heil tala.

2. Tölur geta ekki bæði verið ræðar og óræðar af því þetta eru andstæð hugtök, http://edbook.hi.is/undirbuningur_stae/kafli01/index.html#rauntolurnar-mathbb-r.

3. Ræðu tölurnar eiginlegt hlutmengi í rauntölunum og því eru allar ræðar tölur rauntölur en til eru rauntölur, t.d. \(\pi\) sem ekki eru ræðar.

4. Kvaðratrót náttúrulegra talna geta verið ræðar, t.d. \(\sqrt{9}=3\).

---

1.4. Föll

1.4.1. Skilgreining: Vörpun

Skilgreining

Vörpun en: mapping, record, transform, transformation
Smelltu fyrir ítarlegri þýðingu. frá mengi \(X\) yfir í mengi \(Y\) er regla sem úthlutar sérhverju staki \(x\) í \(X\) nákvæmlega einu staki \(f(x)\) í \(Y\). Táknum þetta með \(f:X \to Y\).

Stakið \(f(x)\) kallast gildi en: image, value
Smelltu fyrir ítarlegri þýðingu. vörpunarinnar (í punktinum \(x\)).

1.4.2. Skilgreining

Skilgreining

Mengið \(X\) kallast skilgreiningarmengi en: argument domain, domain, domain carrier, index set, latent domain, range of arguments, set of definition, source
Smelltu fyrir ítarlegri þýðingu. \(f\), mengið \(Y\) kallast bakmengi en: codomain, latent range, potential range, range, range carrier, target
Smelltu fyrir ítarlegri þýðingu. \(f\) og mengið \(f(X) = \{ f(x); x \in X \}\) kallast myndmengi en: actual range, counterdomain, image, range, right domain
Smelltu fyrir ítarlegri þýðingu. \(f\).

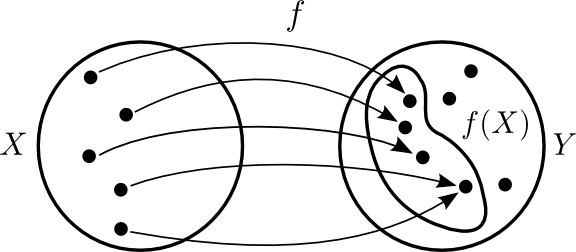
Aðvörun

Það er ekki víst að öll gildin í \(Y\) séu tekin (það er \(f(X)\) getur verið minna en \(Y\)). Eins þá er mögulegt að \(f\) taki sama gildið oftar en einu sinni.

1.4.3. Skilgreining: Samskeyting

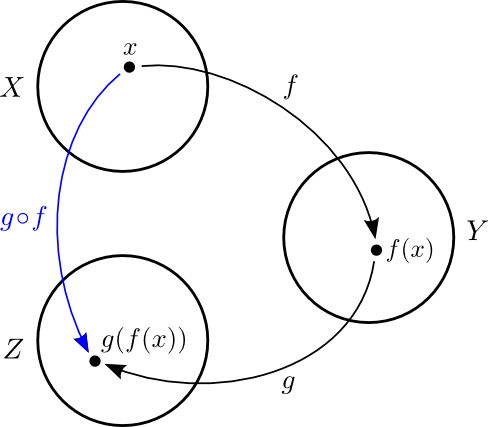
Skilgreining

Látum \(f:X \to Y\) og \(g:Y \to Z\) vera varpanir. Vörpunin \(g\circ f:X \to Z\) sem skilgreind er með \((g\circ f)(x)=g(f(x))\) kallast samskeyting en: composite
Smelltu fyrir ítarlegri þýðingu. \(f\) og \(g\). Stakið \(g(f(x)) \in Z\) fæst með því að beita fyrst vörpuninni \(f\) á stakið \(x\) og síðan vörpuninni \(g\) á stakið \(f(x)\).

1.4.4. Dæmi

Dæmi

Skoðum föllin \(f:\mathbb R \to \mathbb R, f(x) = 2x-1\) og \(g:\mathbb R \to \mathbb R, g(x) = x^2\). Þá er samskeytingin \(g\circ f\)

\[g(f(x)) = g(2x -1) = (2x-1)^2 = 4x^2-4x+1\]

Athugið að samskeytingin \(f \circ g\) er ekki sama fallið

\[f(g(x)) = f(x^2) = 2x^2-1\]

1.4.5. Skilgreining: Átækni og eintækni

Skilgreining

Við segjum að vörpunin \(f\) sé átæk en: surjective, onto
Smelltu fyrir ítarlegri þýðingu. ef \(f(X)=Y\), það þýðir að fyrir sérhvert stak \(y\) í \(Y\) þá er til (amk. eitt) stak \(x\) í \(X\) þannig að \(f(x)=y\).

Segjum að vörpunin \(f\) sé eintæk Ekki fannst þýðing á hugtakinu: eintæk ef \(f(x_1) = f(x_2)\) hefur í för með sér að \(x_1=x_2\), það er sérhvert gildi sem vörpunin tekur er bara tekið einu sinni.

1.4.6. Skilgreining: Gagntækni

Skilgreining

Vörpun sem er bæði eintæk og átæk kallast gagntæk Ekki fannst þýðing á hugtakinu: gagntæk .

1.4.7. Myndband: Varpanir, eintækni og átækni

1.4.8. Skilgreining: Andhverfa

Skilgreining

Látum \(f:X \to Y\) vera vörpun. Sagt er að \(f\) sé andhverfanleg en: invertible, non-singular
Smelltu fyrir ítarlegri þýðingu. ef til er vörpun \(f^{-1}:Y \to X\) þannig að samskeyting varpananna \(f\) og \(f^{-1}\) annars vegar og \(f^{-1}\) og \(f\) hins vegar sé viðeigandi samsemdarvörpun en: identity mapping
Smelltu fyrir ítarlegri þýðingu. , þ.e. \(f^{-1}\circ f=id_X\) og \(f\circ f^{-1} = id_Y\).

Athugasemd

Venjulega hjá okkur þá eru mengin \(X\) og \(Y\) mengi af rauntölum. Þegar \(Y\) er mengi af tölum þá er notast við orðið fall en: function
Smelltu fyrir ítarlegri þýðingu. í stað orðsins vörpun.

1.4.9. Dæmi

Dæmi

Látum \(X=[0,2]\), \(Y=[0,4]\) og \(f:X \to Y, f(x) = x^2\). Þá er \(f\) gagntæk vörpun og andhverfan er gefin með \(f^{-1}(x) = \sqrt x\).

Athugasemd

Hér má velja \(X\) sem önnur mengi en \([0,2]\) svo lengi sem \(X\) inniheldur ekki bæði \(a\) og \(-a\), \(a\neq 0\), því þá er \(f\) ekki lengur eintæk.

Mengið \(Y\) er svo valið sem myndmengið \(f(X)\).

1.4.10. Skilgreining: Graf

Skilgreining

Látum \(f:X \to Y\) vera fall þannig að \(X\) og \(Y\) eru mengi af rauntölum. Graf (e. graph) fallsins \(f\) er þá mengi allra punkta í planinu \(\mathbb{R}^2\) af gerðinni \((x,f(x))\) þar sem \(x\in X\). Hér notum við oft \(y\) í stað \(f(x)\).

1.4.11. Myndband: Föll og gröf

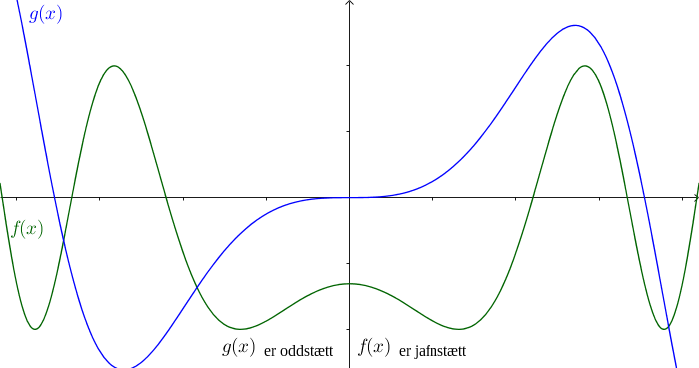
1.4.12. Skilgreining: Jafnstætt og oddstætt

Skilgreining

Við segjum að fall \(f\) sé jafnstætt en: even
Smelltu fyrir ítarlegri þýðingu. ef

\[f(x) = f(-x)\]

fyrir öll \(x\) í skilgreiningarmengi \(f\). Við segjum að fall \(f\) sé oddstætt en: odd
Smelltu fyrir ítarlegri þýðingu. ef

\[f(x) = -f(-x)\]

fyrir öll \(x\) í skilgreiningarmengi \(f\).

1.4.13. Æfingadæmi

Æfingadæmi

Hakið við rétta fullyrðingu.

1. Öll gagntæk föll eiga sér andhverfu.

2. Öll átækt föll eiga sér andhverfu.

3. Fallið \(f: \mathbb{R} \mapsto \mathbb{R_+}\), \(f(x)=\sqrt{x}\) er andhverfa falls \(f: \mathbb{R} \mapsto \mathbb{R_+}\), \(g(x)=x^2\).

4. Til þess að fallið \(f(x)\) geti verið andhverfa fallsins \(g(x)\) verða föllin að hafa sama skilgreiningarmengi.

Lausn

1. Öll gagntæk föll eru andhverfanleg.

2. Ef fallið er ekki eintækt, þ.e. ef til eru punktar \(x_1\neq x_2\) þannig að \(f(x_1)=y=f(x_2)\) þá getum við sagt hvort andhverfan á að taka gildið \(x_1\) eða \(x_2\) í punktinum \(y\).

3. Ef þetta Kvaðratrótin skilar aldrei neikvæðri tölu og því er myndmengi hennar ekki allt \(\mathbb R\) sem er skilgreiningarmengi \(g\).

4. asfd