3. Afleiður
Athugasemd
Nauðsynleg undirstaða
Markgildi. Sjá einnig undirstöðuatriði um markgildi.
Samfelldni. Sjá einnig undirstöðuatriði um samfelld föll.
Samskeyting falla. Sjá einnig undirstöðuatriði um um samskeytingu.
Andhverfur falla. Sjá einnig undirstöðuatriði um andhverfur.
He felt that his whole life was some kind of dream and he sometimes wondered whose it was and whether they were enjoying it.
– Douglas Adams, The Hitchhiker’s Guide to the Galaxy
3.1. Skilgreining á afleiðu
3.1.1. Skilgreining: Afleiða
Skilgreining
Látum \(a\) vera innri punkt skilgreiningarsvæðis falls \(f\).
Afleiða falls
en: derivative
Smelltu fyrir ítarlegri þýðingu.
Ef markgildið er til þá er sagt að fallið \(f\) sé
diffranlegt
en: differentiable
Smelltu fyrir ítarlegri þýðingu.
3.1.2. Dæmi
Dæmi
Fallið \(f(x) = x^2\) er diffranlegt í sérhverjum punkti \(a\). Það sést af því að
3.1.3. Setning
Setning
Ef fall \(f\) er diffranlegt í punkti \(c\) þá er \(f\) samfellt í punktinum \(c\).
Sönnun
Skoðum markgildið \(f'(x)=\lim_{h\to 0} \frac{f(c+h)-f(c)}{h}\). Þar sem \(h\to 0\) þá verður teljarinn einnig að stefna á 0. Það er \(\lim_{h \to 0} f(c+h)-f(c) = 0\), eða \(\lim_{h \to 0} f(c+h) = f(c)\). Þetta má einnig rita \(\lim_{x \to c} f(x) = f(c)\), sem þýðir að fallið \(f\) er samfellt í \(x=c\).
Aðvörun
Fall getur verið samfellt í punkti \(c\) án þess að það sé diffranlegt í \(c\).
3.1.4. Dæmi
Dæmi
Fallið \(f(x) = |x|\) er samfellt. En það er ekki diffranlegt í punktinum \(x=0\). Það sést af því að
en
Þannig að markgildið \(\lim_{h\to 0} \frac{f(0+h)-f(0)}{h}\) er ekki til og því er fallið ekki diffranlegt í \(x=0\).
3.1.5. Snertill
Afleiðu falls \(f\) í punktinum \(a\) fæst með því að taka sniðil (e. secant) í gegnum punktana \((a,f(a))\) og \((a+h,f(a+h))\), og láta svo \(h\) stefna á \(0\).
Þetta gefur hallatölu
snertilsins
en: tangent line, tangent vector
Smelltu fyrir ítarlegri þýðingu.
Jafna snertils við graf fallsins í punktinum \(a\) er línan
3.1.6. Athugasemd: Hallatalan \(\infty\) er ekki leyfð
Athugasemd
Við leyfum ekki \(f'(a) = \infty\) eða \(f'(a) = -\infty\). Samanber \(f(x) = x^{\frac 13}\) í \(a=0\),
Hér ætti því jafna snertilsins að vera \(x=0\).
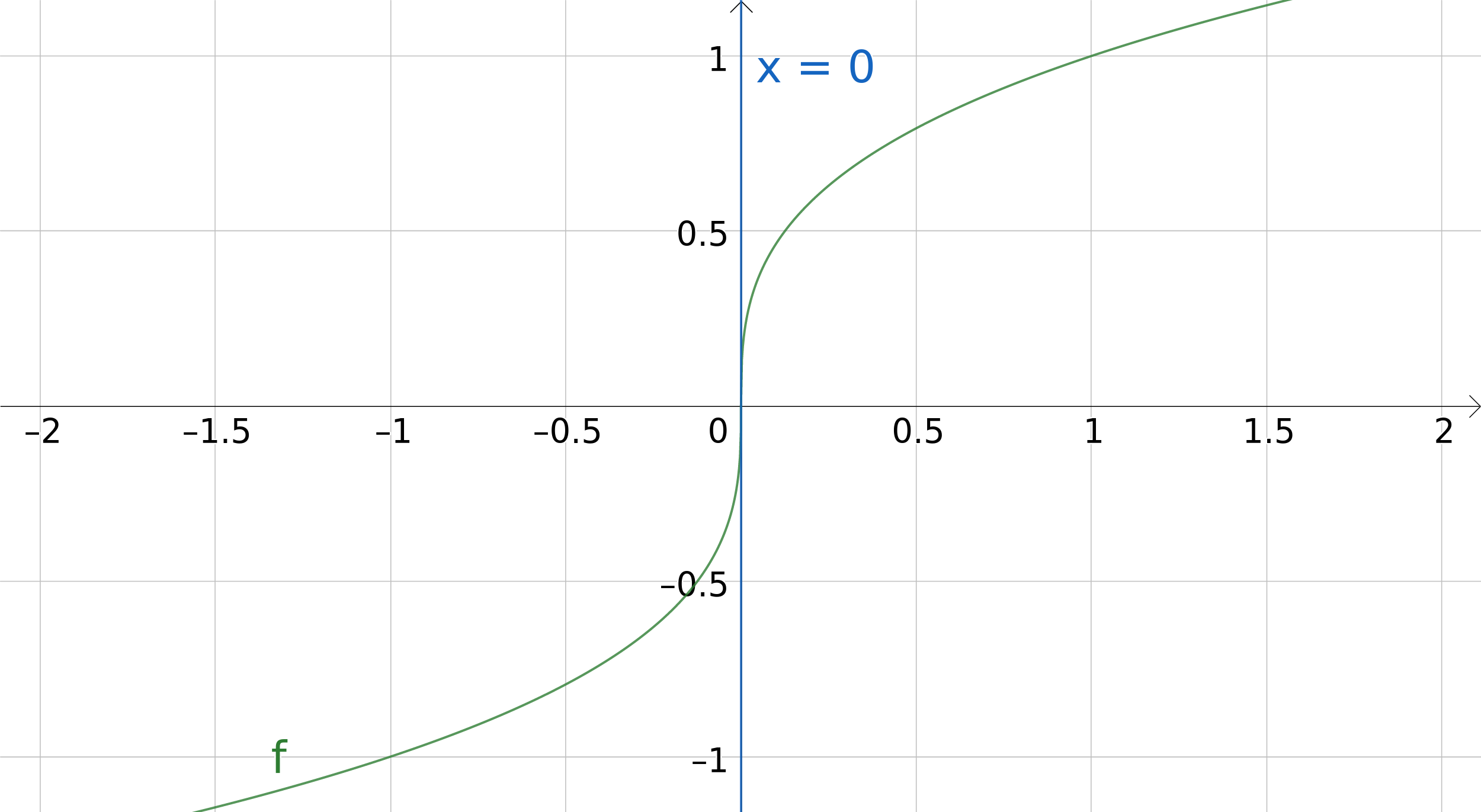
Við viljum að snertillinn sé nálgun við graf fallsins fyrir \(x\) nálægt \(a\), lóðrétt lína er gagnslaus nálgun því hún er ekki skilgreind sem fall af \(x\).
3.2. Útvíkkun fyrir lokuð bil
Ef fallið \(f\) er skilgreint á lokuðu bili þá getum við skilgreint afleiðuna í endapunktunum með því að taka markgildi frá hægri/vinstri eftir því sem við á.
3.2.1. Skilgreining: Hægri/vinstri afleiða
Skilgreining
Hægri afleiða falls \(f\) í punkti \(x\) er skilgreind sem
\[f_+'(x)=\lim_{h\rightarrow 0^+}\frac{f(x+h)-f(x)}{h}.\]Vinstri afleiða falls \(f\) í punkti \(x\) er skilgreind sem
\[f_-'(x)=\lim_{h\rightarrow 0^-}\frac{f(x+h)-f(x)}{h}.\]
3.2.2. Setning
Setning
Ef \(x\) er innri punktur í skilgreiningarsvæði fallsins \(f\) þá er \(f\) diffranlegt í \(x\) þá og því aðeins að
og þá er \(f'(x)\) jafnt og markgildin hér fyrir ofan.
Þetta leiðir beint af skilgreiningunum hér á undan og Setningu 2.2.5.
3.2.3. Skilgreining: Diffranlegt fall
Skilgreining
Látum \(f\) vera fall með skilgreiningarsvæði \(A\). Gerum ráð fyrir að \(A\) sé sammengi endanlega margra bila. Við segjum að fallið \(f\) sé diffranlegt ef það er diffranlegt í öllum innri punktum \(A\) og diffranlegt frá vinstri/hægri í jaðarpunktum \(A\) eftir því sem við á.
3.2.4. Ritháttur
Afleiða falls \(f\) er ýmist táknuð með
Ef við skrifum \(y=f(x)\) þá má einnig tákna hana með
3.2.5. Dæmi
Dæmi
Fallið \(f(x) = \sqrt{x}\), \(f:[0,\infty[\to {{\mathbb R}}\) er diffranlegt á menginu \(]0,\infty[\) og afleiðan er gefin með \(f'(x) = \frac 1{2\sqrt{x}} = \frac 12 x^{-1/2}\) þar. Hins vegar er \(f\) ekki diffranlegt í \(x=0\) þrátt fyrir að fallgildið sé vel skilgreint (og fallið samfellt frá hægri) þar.
Ef \(x>0\) þá fæst
sem segir okkur að \(f'(x) = \frac 12 x^{-1/2}\).
Í vinstri endapunkti skilgreingarsvæðisins, \(x=0\), þá fæst hins vegar
sem sýnir að fallið er ekki diffranlegt frá hægri í \(x=0\).
3.3. Reiknireglur
3.3.1. Setning
Setning
Látum \(f\) og \(g\) vera föll sem eru diffranleg í punkti \(x\). Þá eru föllin \(f+g,\ f-g, kf\) (þar sem \(k\) er fasti) og \(fg\) diffranleg í punktinum \(x\), og ef \(g(x)\neq 0\) þá eru föllin \(1/g\) og \(f/g\) líka diffranleg í \(x\).
Eftirfarandi formúlur gilda um afleiður fallanna sem talin eru upp hér að framan:
\((f+g)'(x)=f'(x)+g'(x)\)
\((f-g)'(x)=f'(x)-g'(x)\)
\((kf)'(x)=kf'(x)\), þar sem \(k\) er fasti
\((fg)'(x)=f'(x)g(x)+f(x)g'(x)\)
\(\displaystyle\Bigg(\frac{1}{g}\Bigg)'(x)=\frac{-g'(x)}{g(x)^2}\), ef \(g(x)\neq 0\)
\(\displaystyle\Bigg(\frac{f}{g}\Bigg)'(x)= \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}\), ef \(g(x)\neq 0\)
3.3.2. Nokkrar afleiður
\(\frac{d}{dx} c = \lim_{h\to 0} \frac{c-c}h = 0\)
\(\frac{d}{dx} x = \lim_{h\to 0} \frac{x+h-x}h = 1\)
\(\frac{d}{dx} x^2 = \lim_{h\to 0} \frac{x^2+2xh+h^2-x^2}h = \lim_{h\to 0} \frac{2xh + h^2}h = \lim_{h\to 0} 2x+h= 2x\)
3.3.3. Setning
Setning
Sönnun
Sýnum þetta með þrepun.Tilfellið \(n=1\) er afgreitt hér að ofan (3.3.2 (2)). Gerum ráð fyrir að niðurstaðan gildi fyrir \(n\) og sýnum að þá gildi hún einnig fyrir \(n+1\),
3.3.4. Afleiður margliða
Með því að nota setningarnar að ofan þá eigum við ekki í neinum vandræðum með að diffra margliður. Setning 3.3.1 (i) segir að við getum diffrað hvern lið fyrir sig, liður (iii) í sömu setningu segir að við getum tekið fastana fram fyrir afleiðuna og loks segir Setning 3.3.3 hvernig við diffrum \(x^n\).
3.3.5. Dæmi: Afleiða margliðu
Dæmi
Finnum afleiðu margliðunnar \(p(x) = 4x^3-2x + 5\). Nú er
3.3.6. Setning: Keðjureglan
Keðjureglan
Gerum ráð fyrir að \(f\) og \(g\) séu föll þannig að \(g\) er diffranlegt í \(x\) og \(f\) er diffranlegt í \(g(x)\). Þá er samskeytingin \(f\circ g\) diffranleg í \(x\) og
3.3.7. Dæmi
Dæmi
Skoðum föllin \(f(x) = \sqrt x\) og \(g(x) = 3x^5\). Bæði þessi föll eru diffranleg og afleiðurnar eru \(f'(x) = \frac 12 x^{-1/2}\) og \(g'(x) = 15x^4\). Afleiða samskeytingarinnar \(f\circ g\) er þá samkvæmt keðjureglunni
3.4. Hærri afleiður
3.4.1. Skilgreining
Skilgreining
Látum \(f\) vera fall. Afleiðan \(f'\) er fall sem skilgreint er í öllum punktum þar sem \(f\) er diffranlegt.
Ef fallið \(f'\) er diffranlegt í punkti \(x\) þá er afleiða \(f'\) í punktinum \(x\) táknuð með \(f''(x)\) og kölluð önnur afleiða (e. second derivative) \(f\) í punktinum \(x\). Líta má á aðra afleiðu \(f\) sem fall \(f''\) sem er skilgreint í öllum punktum þar sem \(f'\) er diffranlegt.
Almennt má skilgreina \(n\)-tu afleiðu \(f\), táknaða með \(f^{(n)}\), þannig að í þeim punktum \(x\) þar sem fallið \(f^{(n-1)}\) er diffranlegt þá er \(f^{(n)}(x)=\frac{d}{dx}f^{(n-1)}(x)\).
3.4.2. Dæmi
Dæmi
Ef \(f(x) = 3x^2\), þá er
og
3.4.3. Ritháttur
Ritum \(y=f(x)\).
Þá má tákna fyrstu afleiðu \(f\) með
aðra afleiðuna með
og almennt \(n\)-tu afleiðuna
Athugasemd
Venja er að rita \(f'''\) til að tákna þriðju afleiðu \(f\) en afar sjaldgæft að \(f''''\) sé notað til að tákna fjórðu afleiðu \(f\) og mun algengara að nota \(f^{(4)}\).
3.5. Útgildi
3.5.1. Skilgreining: Útgildi
Skilgreining
Við segjum að fall \(f\) hafi
staðbundið hágildi
en: local maximum, maximum, maximum in the small, relative maximum
Smelltu fyrir ítarlegri þýðingu.
Við segjum að fall \(f\) hafi
staðbundið lággildi
en: local minimum, minimum, minimum in the small, relative minimum
Smelltu fyrir ítarlegri þýðingu.
Tölum um að fallið \(f\) hafi
staðbundið útgildi
en: extremum in the small, local extremum, relative extremum
Smelltu fyrir ítarlegri þýðingu.
3.5.2. Setning
Setning
Ef fallið \(f\) hefur staðbundið útgildi í punktinum \(x_0\) og er diffranlegt þá er \(f'(x_0)=0\).
Sönnun
Gerum ráð fyrir að \(f\) hafi staðbundið hágildi í punktinum \(x_0\). Þá er \(f(x_0)-f(x)\geq 0\) og ef \(x<x_0\), þá fæst að \(\frac{f(x_0)-f(x)}{x_0-x}\geq 0\). Þetta þýðir að
Eins þá er \(f(x_0)-f(x)\geq 0\) og ef \(x_0<x\), þá er \(\frac{f(x_0)-f(x)}{x_0-x} \leq 0\). Þetta þýðir að
Við vitum að markgildið \(\lim_{x\to x_0} \frac{f(x_0)-f(x)}{x_0-x}\) er til þar sem fallið er diffranlegt, það þýðir að markgildin frá hægri og vinstri eru þau sömu. Eina leiðin til þess að það samræmist hægri og vinstri markgildunum hér að ofan er ef
Aðvörun
Þó að \(f'(a)=0\) þá er ekki víst að \(a\) sé staðbundið útgildi.
Til dæmis þá hefur fallið \(f(x) = x^3\) ekkert staðbundið útgildi þrátt fyrir að \(f'(0) = 0\) (\(f'(x) = 3x^2\)).
3.6. Hornaföll og afleiður þeirra
3.6.1. Setning
Setning
\(\displaystyle\lim_{x\rightarrow 0}\frac{\sin x}{x}=1\)
\(\displaystyle\lim_{x\rightarrow 0}\frac{\cos x-1}{x}=0\)
\(\displaystyle\frac{d}{dx}\sin x=\cos x\)
\(\displaystyle\frac{d}{dx}\cos x=-\sin x\)
\(\displaystyle\frac{d}{dx}\tan x=\frac{1}{\cos^2 x}=1+\tan^2 x\)
3.7. Meðalgildissetningin
3.7.1. Setning Rolle
Setning Rolle
Látum \(g:[a,b]\rightarrow{{\mathbb R}}\) vera samfellt fall. Gerum ráð fyrir að \(g\) sé diffranlegt í öllum punktum í bilinu \((a,b)\). Ef \(g(a)=g(b)\) þá er til punktur \(c\) á bilinu \((a,b)\) þannig að \(g'(c)=0\).
Sönnun
Ef \(g(x)=c\) er fasti, þá er \(g'(x)=0\). Ef hins vegar \(g\) er ekki fasti þá er til \(x \in (a,b)\) þannig að \(g(x)\neq g(a)\), gerum ráð fyrir að \(g(x)>g(a)\) (tilfellið ef \(g(x)<g(a)\) gengur nánast eins fyrir sig). Samkvæmt Há- og lággildislögmálinu þá tekur fallið \(g\) sitt hæsta gildi í punkti \(c\) á bilinu \([a,b]\).Þar sem \(g(c)\geq g(x) > g(a) = g(b)\) þá getur \(c\) hvorki verið \(a\) né \(b\). Þar sem \(c\) er útgildi þá segir Setning 3.5.2 að \(g'(c)=0\).
3.7.2. Meðalgildissetningin
Meðalgildissetningin
Látum \(f:[a,b]\rightarrow{{\mathbb R}}\) vera samfellt fall. Gerum ráð fyrir að \(f\) sé diffranlegt í öllum punktum í bilinu \((a,b)\). Þá er til punktur \(c\) í bilinu \((a,b)\) þannig að
Sönnun
Skilgreinum nýtt fall
Athugið að \(h\) er bara \(f\) mínus
línufallið
en: affine function
Smelltu fyrir ítarlegri þýðingu.
Nú er
þannig að
eða
Athugasemd
Niðurstöðuna úr
meðalgildissetningunni
en: mean value theorem
Smelltu fyrir ítarlegri þýðingu.
Í einhverjum punkti á bilinu er stundarbreytingin jöfn meðalbreytingunni yfir allt bilið.
3.7.3. Alhæfða meðalgildissetningin
Setning
Gerum ráð fyrir að föllin \(f\) og \(g\) séu samfelld á lokaða bilinu \([a,b]\) og diffranleg á opna bilinu \((a,b)\). Gerum auk þess ráð fyrir að fyrir allar tölur \(x\) í \((a,b)\) sé \(g'(x)\neq 0\). Þá er til tala \(c\in (a,b)\) þannig að
3.8. Vaxandi og minnkandi föll
3.8.1. Skilgreining: Vaxandi/minnkandi
Skilgreining
Fall \(f\) er vaxandi á bili \((a,b)\) ef um alla punkta \(x_1\) og \(x_2\) á \((a,b)\) þannig að \(x_1 < x_2\) gildir að
Fall \(f\) er stranglega vaxandi á bili \((a,b)\) ef um alla punkta \(x_1\) og \(x_2\) á \((a,b)\) þannig að \(x_1 < x_2\) gildir að
Fall \(f\) er minnkandi á bili \((a,b)\) ef um alla punkta \(x_1\) og \(x_2\) á \((a,b)\) þannig að \(x_1 < x_2\) gildir að
Fall \(f\) er stranglega minnkandi á bili \((a,b)\) ef um alla punkta \(x_1\) og \(x_2\) á \((a,b)\) þannig að \(x_1 < x_2\) gildir að
Athugasemd
Kennslubókin notar nondecreasing/nonincreasing fyrir vaxandi/minnkandi og increasing/decreasing fyrir stranglega vaxandi/minnkandi.
Einnig þekkist að nota increasing/decreasing og strictly increasing/decreasing. Til dæmis er það gert á Wikipedia: Monotonic functions.
3.8.2. Setning
Setning
Látum \(f\) vera diffranlegt fall á bili. Þá er \(f\) vaxandi þá og því aðeins að \(f' \geq 0\).
Sönnun
Byrjum á að gera ráð fyrir að fallið sé vaxandi. Festum punkt \(x\) og sýnum að \(f'(x)\geq 0\). Þar sem \(f\) er vaxandi þá gildir fyrir sérhvert \(h>0\) að
Þá gildir einnig um markgildið \(\lim_{h\to 0^+} \frac{f(x+h)-f(x)}h \geq 0\).
Ef hins vegar \(h<0\) þá er \(x+h < x\) og því \(f(x+h)<f(x)\). Þetta gefur að
sem þýðir að \(\lim_{h\to 0^-} \frac{f(x+h)-f(x)}h \geq 0\). Og þar af leiðandi er \(f'(x) = \lim_{h\to 0} \frac{f(x+h)-f(x)}h \geq 0\).
Gerum nú ráð fyrir \(f'\geq 0\) og sýnum að þá sé fallið vaxandi. Festum tvo punkta \(x_1 < x_2\). Ef \(f(x_1) > f(x_2)\), það er \(f(x_2)-f(x_1)<0\) þá er
Samkvæmt meðalgildissetningunni þá er til punktur \(¢\) á bilinu \([x_1,x_2]\) þar sem afleiðan tekur þetta gildi, en það er í mótsögn við að \(f'(c)\geq 0\).
3.8.3. Setning
Setning
Látum \(f\) vera diffranlegt fall á bili. Þá er \(f\) minnkandi þá og því aðeins að \(f' \leq 0\).
3.8.4. Setning
Setning
Látum \(f\) vera diffranlegt fall á bili. Ef \(f'>0\) þá er \(f\) stranglega vaxandi.
3.8.5. Setning
Setning
Látum \(f\) vera diffranlegt fall á bili. Ef \(f'<0\) þá er \(f\) stranglega minnkandi.
Aðvörun
Diffranlegt fall getur verið stranglega vaxandi/minnkandi án þess að afleiðan sé alls staðar stærri/minni en 0. Til dæmis er afleiða \(f(x)=x^3\) jöfn 0 í \(x=0\) en fallið er stranglega vaxandi á öllum rauntalnaásnum.
3.8.6. Afleiður fastafalla
Við vitum að ef \(f\) er fasti, það er \(f(x)=c\), þá er \(f'(x)=0\) fyrir öll \(x\).
Nú fáum við einnig eftirfarandi út frá Setningum 3.8.2 og 3.8.3:
Ef \(f\) er diffranlegt fall á bili \(I\) sem er þannig að \(f'(x) = 0\) á \(I\), þá er \(f\) fasti, þ.e. \(f(x) = c\) fyrir öll \(x\in I\).
3.9. Fólgin diffrun
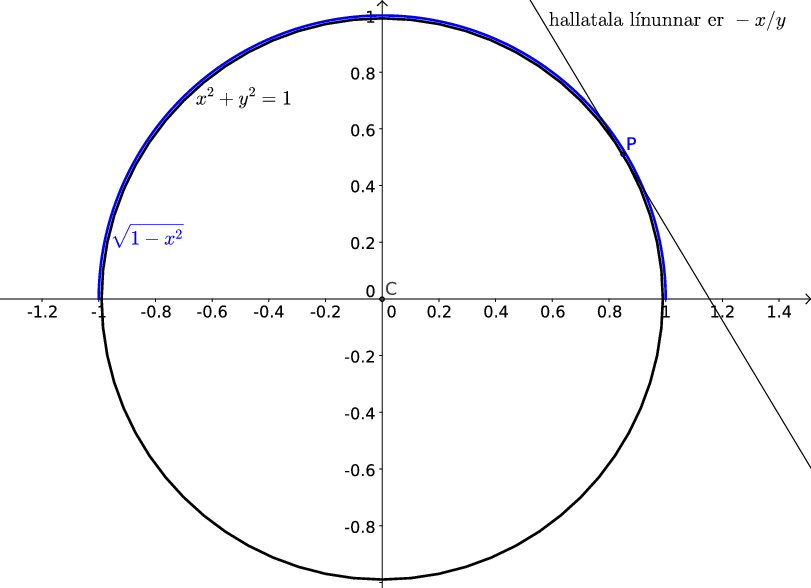
3.9.1. Dæmi
Dæmi
Jafna hrings með geisla 1 er \(x^2+y^2=1\). Við vitum að hægt er að skrifa efri og neðri helminga hans sem föll af \(y\), annars vegar \(y=\sqrt{1-x^2}\) og hins vegar \(y=-\sqrt{1-x^2}\). Ef við viljum finna snertil við hringinn getum við notað þessi föll. En þar sem við vitum að hægt er að skrifa \(y\) sem fall af \(x\) þá getum við einnig diffrað jöfnu hringsins beint með aðstoð keðjureglunnar,
3.9.2. Setning: Andhverfusetningin
Setning
Látum feril vera gefinn með \(F(x,y) =0\), þar sem \(F\) er diffranlegt í bæði \(x\) og \(y\). Í punktum þar sem snertill ferilsins er ekki lóðréttur (þ.e. \(\frac{d}{dy}F \neq 0\)) þá er hægt að skrifa \(y\) sem fall af \(x\) og þá fæst af keðjureglunni að
þ.e.
3.9.3. Með öðrum orðum
Það kemur í sama stað niður að einangra \(y=f(x)\), ef það er mögulegt, og finna \(y'\) með því að diffra, eins og að diffra \(F(x,y)=0\) og einangra svo \(y'=\frac{dy}{dx}\).
3.9.4. Vinnulag
Diffrum báðar hliðar jöfnunar með tilliti til \(x\), og lítum á \(y\) sem fall af \(x\) sem við diffrum með aðstoð keðjureglunnar (og gleymum ekki \(y'\))
Einangrum \(y'\)
Skiptum \(y\) út fyrir \(f(x)\).
3.9.5. Setning: Hagnýting á fólginni diffrun
Setning
Ef \(n\) og \(m\) eru heilar tölur þá er
Sönnun
Punktar á grafi fallsins \(x^{n/m}\) ákvarðast af jöfnunni \(y=x^{n/m}\), það er \(y^m = x^n\). Skilgreinum því
Þar sem \(\frac d{dx} F(x,y) = nx^{n-1}\) og \(\frac d{dy} F(x,y) = -my^{m-1}\) þá fæst að
3.10. Andhverf föll
Rifjum upp að gagntæk vörpun \(f:X\to Y\) hefur andhverfu \(f^{-1}:Y\to X\) sem uppfyllir að
Sjá kafla 1.4.
3.10.1. Athugasemd
Athugasemd
Látum \(f:X \to Y\) vera fall sem skilgreint er á mengi \(X\). Gerum ráð fyrir að \(f\) sé eintækt. Með því að einskorða bakmengi \(f\) við myndmengið \(\tilde Y = f(X)\) þá verður \(f:X\to \tilde Y\) gagntækt fall. Þá er til andhverfa \(f^{-1}:\tilde Y \to X\) sem uppfyllir
3.10.2. Setning
Setning
Fall sem er strangt vaxandi eða strangt minnkandi er eintækt og á sér því andhverfu.
3.10.3. Eiginleikar andhverfra falla
\(y=f^{-1}(x)\) þá og því aðeins að \(x=f(y)\).
Skilgreingarsvæði \(f\) er myndmengi \(f^{-1}\).
Myndmengi \(f^{-1}\) er jafnt skilgreiningarsvæði \(f\).
\(f^{-1}(f(x))=x\) fyrir öll \(x\) í skilgreiningarsvæði \(f\).
\(f(f^{-1}(x))=x\) fyrir öll \(x\) í skilgreiningarsvæði \(f^{-1}\).
\((f^{-1})^{-1}(x)=f(x)\) fyrir öll \(x\) í skilgreiningarsvæði \(f\), alltsvo \((f^{-1})^{-1}=f\).
Graf \(f^{-1}\) er speglun á grafi \(f\) um línuna \(y=x\).
3.10.4. Setning: Afleiða andhverfunnar
Setning
Gerum ráð fyrir að fall \(f\) hafi andhverfu \(f^{-1}\). Látum \(x\) vera á skilgreiningarsvæði \(f\) og gerum ráð fyrir að \(f\) sé diffranlegt í punktinum \(f^{-1}(x)\) og að \(f'(f^{-1}(x)) \neq 0\). Þá er \(f^{-1}\) diffranlegt í punktinum \(x\) og
Athugasemd
Setningin segir okkur sér í lagi að láréttur snertill við \(f\) svarar til lóðrétts snertils við \(f^{-1}\).
3.11. Línulegar nálganir
3.11.1. Staðbundnar nálganir
Skoðum diffranlegt fall \(f\) í grennd um fastan punkt \(a\). Látum \(x\) vera punkt í grennd um \(a\). Ef graf fallsins er ekki „mjög sveigt“ þá er snertillinn við \((a,f(a))\) næstum samsíða sniðlinum gegnum \((a,f(a))\) og \((x,f(x))\). Það þýðir að
Aðvörun
Athugið að hér er \(a\) fast en \(x\) breytist.
Athugasemd
Einnig er hægt að skrifa þetta á eftirfarandi hátt. Setjum \(\Delta x = x-a\) og \(\Delta y = f(x) - f(a)\) þá þýðir þetta að \(\Delta y \approx \Delta x f'(a)\).
Það er, breytingin á fallgildinum er um það bil breytingin í breytunni margfaldað við afleiðuna í punktinum.
3.11.2. Skilgreining: Línuleg nálgun
Skilgreining
Línuleg nálgun á falli \(f\) nálægt \(a\), eða 1. stigs Taylor-margliða \(f\) í \(a\), er gefin með \(P_1(x)=f(a)+f'(a)(x-a)\).
3.11.3. Setning: Skekkjumat
Setning
Skekkjan í nálguninni \(E_1(x)=f(x)-P_1(x)\) uppfyllir að til er tala \(X \in (a,x)\) þannig að
3.11.4. Skekkjumat fyrir línulegar nálganir
Gerum ráð fyrir að \(f''(t)\) sé skilgreint fyrir öll \(t\) í opnu bili sem inniheldur bæði \(a\) og \(x\). Gerum enn fremur ráð fyrir að \(m\) og \(M\) séu tölur þannig að fyrir öll \(t\in (a, x)\) gildi að \(m\leq f''(t)\leq M\). Þá er
sem gefur að
3.12. Taylor-margliður
Línuleg nálgun á falli er ekkert annað en nálgun með fyrsta stigs margliðu.
Spurningin er því hvort hægt sé að nota margliður af hærra stigi og fá þá betri nálgun?
Hvernig er 0. stigs nálgun á falli?
3.12.1. Skilgreining: Taylor-margliða
Skilgreining
Gerum ráð fyrir að fall \(f\) sé diffranlegt \(n\) sinnum í punkti \(a\), þ.e.a.s. við gerum ráð fyrir að \(n\)-ta afleiðan \(f^{(n)}(a)\) sé skilgreind. Taylor margliða af \(n\)-ta stigi fyrir \(f\) um \(x=a\) (oft líka sagt með miðju í \(a\)) er margliðan
Talað er um \(n\)-ta stigs Taylor-nálgun þegar gildið \(P_n(x)\) er notað sem nálgun fyrir \(f(x)\).
Skekkjan í nálguninni (munurinn á réttu fallgildi og nálgunargildi) er táknaður með
3.12.2. Skekkjumat fyrir Taylor-margliður
Gerum ráð fyrir að \(n+1\)-afleiðan \(f^{(n+1)}(t)\) sé skilgreind fyrir öll \(t\) í opnu bili sem inniheldur bæði \(a\) og \(x\). Þá er til tala \(X\) á milli \(a\) og \(x\) þannig að
Því má rita
Aðvörun
Yfirleitt er engin leið til þess að finna \(X\). Hins vegar getum við haft gagn af skekkjumatinu ef við höfum mat á \(f^{(n+1)}\).
3.12.3. Fylgisetning
Fylgisetning
Gerum ráð fyrir að \(f\) sé \(n+1\) diffranlegt á bili sem inniheldur bæði \(a\) og \(x\). Gerum enn fremur ráð fyrir að \(m\) og \(M\) séu tölur þannig að fyrir öll \(t\) á milli a og x gildi að \(m\leq f^{(n+1)}(t)\leq M\). Þá er
3.12.4. Ritháttur
Við ritum
ef til er fasti \(K\) og tala \(\delta>0\) þannig að
Einnig er ritað
ef \(f(x)-g(x)=O(u(x))\) þegar \(x\rightarrow a\).
Tilgangur þessa ritháttar er að skilgreina tól sem getur sagt okkur hversu hratt \(f\) stefnir á markgildið þegar \(x\to a\).
3.12.5. Athugasemd
Athugasemd
Við sjáum að
því hægt er að nota \(K = \frac{\max\{-m,M\}}{(n+1)!}\) í skilgreiningunni hér á undan.
3.12.6. Setning
Setning
Gerum ráð fyrir að \(Q_n(x)\) sé margliða af stigi ekki hærra en \(n\). Ef \(f(x)=Q_n(x)+O((x-a)^{n+1})\) þegar \(x\rightarrow a\) þá er \(Q_n(x)=P_n(x)\) þar sem \(P_n(x)\) er \(n\)-ta stigs Taylor-margliða \(f\) með miðju í \(a\).
Með öðrum orðum, \(P_n\) er sú margliða af stigi \(\leq n\) sem nálgar \(f\) best.
3.13. Regla l’Hôpital
3.13.1. Regla l’Hôpital, einhliða útgáfa
Setning
Gerum ráð fyrir að föllin \(f\) og \(g\) séu diffranleg á opnu bili \((a, b)\) og að \(g'(x)\neq 0\) fyrir öll \(x\in (a, b)\). Gerum enn fremur ráð fyrir að
(Hér má \(L\) vera rauntala, \(\infty\) eða \(-\infty\).)
Þá er
Eins má skoða markgildi frá vinstri \(x\to a^-\).
Sönnun
Þar sem \(\lim_{x\rightarrow a^+}f(x)=\lim_{x\rightarrow a^+}g(x)=0\) þá getum við gert ráð fyrir að \(f\) og \(g\) séu samfelld á bilinu \([a,b)\) og taki gildið 0 í \(a\).
Þá fæst af alhæfðu meðalgildissetningunni fyrir sérhvert \(x\in (a,b)\) að til er \(c \in (a,x)\) þannig að
Þegar \(x \to a^+\) þá gildir einnig að \(c \to a^+\) því \(c\) er klemmt á milli \(a\) og \(x\). Þar sem markgildið
er til, þá er markgildið \(\lim_{x\rightarrow a^+}\frac{f(x)}{g(x)}\) einnig til og er jafnt og \(L\).
3.13.2. Regla l’Hôpital
Setning
Gerum ráð fyrir að föllin \(f\) og \(g\) séu diffranleg á bilum \((x_1, a)\) og \((a, x_2)\) og að \(g'(x)\neq 0\) fyrir öll \(x\) í þessum bilum. Gerum enn fremur ráð fyrir að
(Hér má \(L\) vera rauntala, \(\infty\) eða \(-\infty\).)
Þá er
3.13.3. Dæmi
Dæmi
Við höfum áður séð að \(\lim_{x\to 0} \sin(x)/x = 1\). Skoðum hvernig hægt er að sýna þetta með lítilli fyrirhöfn og reglu l’Hôpital.
Sjáum að \(f(x) = \sin(x)\) og \(g(x) = x\) eru diffranleg í grennd um 0 og að \(g'(x) = 1 \neq 0\). Þá fæst að
3.13.4. Regla l’Hôpital, \(\infty\)-útgáfa
Setning
Gerum ráð fyrir að föllin \(f\) og \(g\) séu diffranleg á bilum \((x_1, \infty)\) og að \(g'(x)\neq 0\) fyrir öll \(x\in (x_1, \infty)\). Gerum enn fremur ráð fyrir að
(Hér má \(L\) vera rauntala, \(\infty\) eða \(-\infty\).)
Þá er
3.13.5. Regla l’Hôpital, tvíhliða útgáfa
Setning
Gerum ráð fyrir að föllin \(f\) og \(g\) séu diffranleg á bilum \((x_1, a)\) og \((a, x_2)\) og að \(g'(x)\neq 0\) fyrir öll \(x\) í þessum bilum. Gerum enn fremur ráð fyrir að
(Hér má \(L\) vera rauntala, \(\infty\) eða \(-\infty\).)
Þá er