2. Markgildi og samfelldni
Athugasemd
Nauðsynleg undirstaða
Aðvörun
Þessi kafli fjallar um tvö afskaplega mikilvæg og nátengd hugtök, markgildi og samfelldni. Það er nauðsynlegt fyrir nemendur að ná góðum tökum á þeim því mörg hugtök í stærðfræði og hagnýtingum á stærðfræði sem verða á vegi ykkar í framtíðinni byggja á þessum hugtökum.
I’d take the awe of understanding over the awe of ignorance any day.
- Douglas Adams, The Salmon of Doubt
2.1. Markgildi
2.1.1. Óformleg skilgreining á markgildi
Segjum að fall \(f(x)\) stefni á tölu \(L\) þegar \(x\) stefnir á \(a\), og ritum \(\lim_{x\rightarrow a} f(x)=L\), ef við getum tryggt að \(f(x)\) sé eins nálægt \(L\) og við viljum bara með því að velja \(x\) nógu nálægt \(a\).
2.1.2. Skilgreining: Markgildi
Skilgreining
Gerum ráð fyrir að fall \(f\) sé skilgreint á opnu bili umhverfis punktinn \(a\), nema hvað hugsanlega er \(f(a)\) ekki skilgreint. Við segjum að \(f(x)\) stefni á tölu \(L\) þegar \(x\) stefnir á \(a\), og ritum \(\lim_{x\rightarrow a} f(x)=L\), ef eftirfarandi skilyrði er uppfyllt:
Fyrir sérhverja tölu \(\epsilon>0\) er til tala \(\delta>0\) sem fullnægir eftirfarandi skilyrði:
Við segjum að talan \(L\) sé
markgildi
en: limit
Smelltu fyrir ítarlegri þýðingu.
Athugasemd
Þegar athugað er hvort markgildið \(\lim_{x\rightarrow a} f(x)\) er til, og þá hvert gildi þess er, þá skiptir ekki máli hvort \(f(a)\) er skilgreint eða ekki.
2.1.3. Dæmi um markgildi
Dæmi
Látum \(a, c\) vera rauntölur. Sýnið fram á eftirfarandi:
\(\lim_{x \to a}\,c = c\),
\(\lim_{x \to a}\,x = a\)
\(\lim_{x \to a} |x| = |a|\)
Lausn á lið 2
Hér er fallið sem um ræðir \(f(x) = x\) og \(L=a\). Látum \(\epsilon>0\) vera gefið. Við viljum finna \(\delta >0\) þannig að \(|x-a|<\delta\) hafi í för með sér \(|f(x)-a| < \epsilon\). Þar sem \(f(x)=x\) þá er seinni ójafnan jafngild \(|x-a|<\epsilon\). Þetta er sama ójafnan og \(\delta\) þarf að uppfylla þannig að okkur nægir að velja \(\delta = \epsilon\). Þá hefur
í för með sér að
Ábendingar fyrir liði 1 og 3
Til að sanna þetta þá er best að teikna mynd til að átta sig á því hvernig föllin haga sér. Svo má velja
\(\delta\) sem hvað sem er.
\(\delta=\epsilon\).
2.2. Markgildi frá hægri og vinstri
2.2.1. Óformleg skilgreining á markgildi frá hægri
Gerum ráð fyrir að fall \(f\) sé skilgreint á opnu bili \((a,b)\). Segjum að \(f(x)\) stefni á tölu \(L\) þegar \(x\) stefnir á \(a\) frá hægri, og ritum \(\lim_{x\rightarrow a^+} f(x)=L\), ef við getum tryggt að \(f(x)\) sé eins nálægt \(L\) og við viljum bara með því að velja \(x>a\) nógu nálægt \(a\).
2.2.2. Skilgreining: Markgildi frá hægri
Skilgreining
Gerum ráð fyrir að fall \(f\) sé skilgreint á opnu bili \((a,b)\). Við segjum að \(f(x)\) stefni á tölu \(L\) þegar \(x\) stefnir á \(a\) frá hægri, og ritum \(\lim_{x\rightarrow a^+} f(x)=L\), ef eftirfarandi skilyrði er uppfyllt.
Fyrir sérhverja tölu \(\epsilon>0\) er til tala \(\delta>0\) þannig að um öll \(x\) sem eru þannig að
2.2.3. Óformleg skilgreining á markgildi frá vinstri
Gerum ráð fyrir að fall \(f\) sé skilgreint á opnu bili \((b,a)\). Segjum að \(f(x)\) stefni á tölu \(L\) þegar \(x\) stefnir á \(a\) frá vinstri, og ritum \(\lim_{x\rightarrow a^-} f(x)=L\), ef við getum tryggt að \(f(x)\) sé eins nálægt \(L\) og við viljum bara með því að velja \(x<a\) nógu nálægt \(a\).
2.2.4. Skilgreining: Markgildi frá vinstri
Skilgreining
Gerum ráð fyrir að fall \(f\) sé skilgreint á opnu bili \((b,a)\). Við segjum að \(f(x)\) stefni á tölu \(L\) þegar \(x\) stefnir á \(a\) frá vinstri, og ritum \(\lim_{x\rightarrow a^-} f(x)=L\), ef eftirfarandi skilyrði er uppfyllt.
Fyrir sérhverja tölu \(\epsilon>0\) er til tala \(\delta>0\) þannig að um öll \(x\) sem eru þannig að
2.2.5. Setning
Setning
Gerum ráð fyrir að fall \(f\) sé skilgreint á opnu bili umhverfis punktinn \(a\), nema hvað hugsanlega er \(f(a)\) ekki skilgreint. Þá er
ef og aðeins ef
2.2.6. Dæmi: Tölugildisfallið
Dæmi
Tölugildisfallið
en: absolute value, length, modulus, norm, numerical value
Smelltu fyrir ítarlegri þýðingu.
- \[\lim_{x\to 0^+} \frac x{|x|} = 1\]
- \[\lim_{x\to 0^-} \frac x{|x|} = -1\]
- \[\lim_{x\to 0} \frac x{|x|} \quad \text{er ekki til}\]
Lausn
Hér skoðum við eingöngu \(x>0\) og þá gildir að \(\frac x{|x|} = \frac xx = 1\). Þar sem \(\lim_{x \to 0} 1 = 1\) samkvæmt Dæmi 2.1.3 þá gildir einni að \(\lim_{x \to 0^+} 1 = 1\) samkvæmt setningunni hér á undan. Þannig að
\[\lim_{x \to 0^+} \frac x{|x|} = \lim_{x \to 0^+} 1 = 1\]Eins og liður 1 nema ef \(x<0\) þá er \(\frac x{|x|} = \frac x{-x} = -1\)
Af liðum 1 og 2 sést að hægri og vinstri markgildin eru ekki þau sömu þannig að samkvæmt setningunni hér á undan þá er markgildið ekki til.

2.3. Reiknireglur fyrir markgildi
2.3.1. Setning
Setning
Gerum ráð fyrir að \(\lim_{x\rightarrow a}f(x)=L\) og að \(\lim_{x\rightarrow a}g(x)=M\). Þá gildir
\(\lim_{x\rightarrow a}\Big(f(x)+g(x)\Big)=L+M\).
\(\lim_{x\rightarrow a}\Big(f(x)-g(x)\Big)=L-M\).
\(\lim_{x\rightarrow a}f(x)g(x)=LM\).
\(\lim_{x\rightarrow a}kf(x)=kL\), þar sem \(k\) fasti.
\(\lim_{x\rightarrow a}f(x)/g(x)=L/M\), að því gefnu að \(M\neq 0\).
Gerum ráð fyrir að \(m\) og \(n\) séu heiltölur þannig að \(f(x)^{m/n}\) sé skilgreint fyrir öll \(x\) á bili \((b,c)\) umhverfis \(a\) (en ekki endilega fyrir \(x=a\)) og að \(L^{m/n}\) sé skilgreint. Þá er \(\lim_{x\rightarrow a}f(x)^{m/n}=L^{m/n}\).
Ef til er bil \((b,c)\) sem inniheldur \(a\) þannig að \(f(x)\leq g(x)\) fyrir öll \(x\in (b,c)\), nema kannski \(x=a\), þá er \(\lim_{x\rightarrow a}f(x)=L\leq M=\lim_{x\rightarrow a}g(x)\).
Sönnun á lið 1
Við viljum sýna að fyrir \(\epsilon>0\) þá sé til \(\delta>0\) þannig að ef \(|x-a|<\delta\) þá sé \(|f(x)+g(x) - (L+M)|<\epsilon\). Látum nú \(\epsilon>0\) vera gefið, þá fæst af \(\lim_{x\to a} f(x) = L\) að til er \(\delta_1>0\) þannig að
ef \(|x-a|<\delta_1\). Eins fæst af \(\lim_{x \to a} g(x)=M\) að til er \(\delta_2\) þannig að
ef \(|x-a|<\delta_2\).
Ef við setjum \(\delta = \min\{\delta_1,\delta_2\}\) þá þýðir það að öll \(x\) sem uppfylla \(|x-a|<\delta\) uppfylla einnig \(|x-a|<\delta_1\) og \(|x-a|<\delta_2\). Þá gefur þríhyrningsójafnan okkur að fyrir slíkt \(x\) þá er
sem er það sem við vildum sýna.
Aðvörun
Liður (1) í setningunni á undan segir að ef markgildin \(\lim_{x\to a} f(x)\) og \(\lim_{x\to a} g(x)\) eru til þá sé markgildið \(\lim_{x\to a} (f(x)+g(x))\) einnig til.
En hún segir ekki að ef \(f\) og \(g\) eru föll þannig að markgildið \(\lim_{x\to a} (f(x)+g(x))\) er til, að þá séu markgildin \(\lim_{x\to a} f(x)\) og \(\lim_{x\to a} g(x)\) einnig til.
2.3.2. Setning: Klemmureglan
Setning
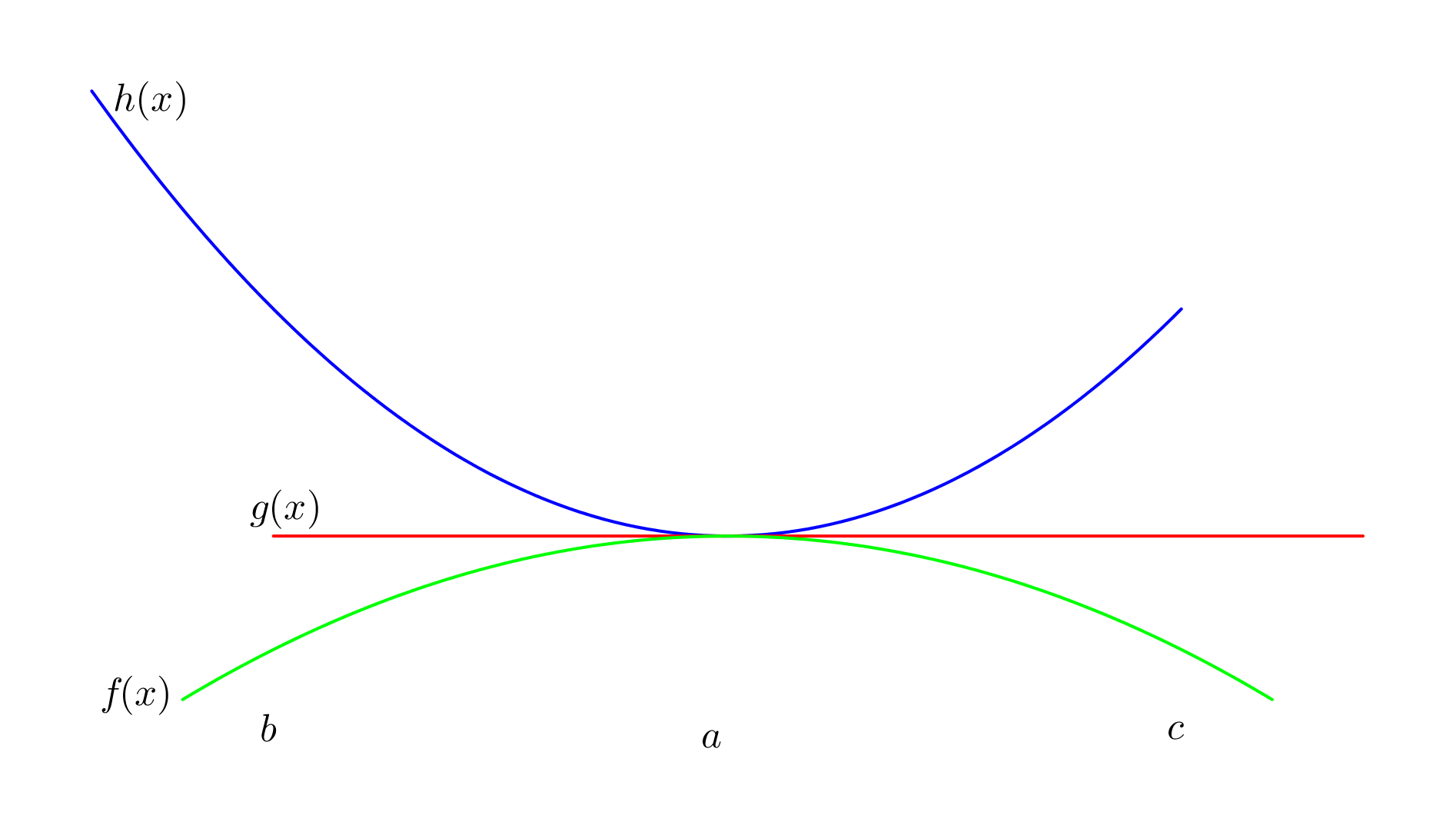
Gerum ráð fyrir að \(f(x)\leq g(x)\leq h(x)\) fyrir öll \(x\) á bili \((b, c)\) sem inniheldur \(a\), nema kannski \(x=a\). Gerum enn fremur ráð fyrir að
Þá er \(\lim_{x\rightarrow a}g(x)=L\).
Sönnun
Látum \(\epsilon>0\) vera gefið. Við viljum sýna að þá sé til \(\delta>0\) þannig að \(|g(x)-L|<\epsilon\) fyrir öll \(x\) sem uppfylla \(|x-a|<\delta\).
Þetta má líka skrifa svona: Við viljum sýna að þá sé til \(\delta>0\) þannig að \(L-\epsilon<g(x)<L+\epsilon\) fyrir öll \(x\) sem uppfylla \(a-\delta < x<a+\delta\).
Við vitum nú að þar sem \(\lim_{x\to a} f(x) = L\) þá er til \(\delta_1\) þannig að \(L-\epsilon<f(x)<L+\epsilon\) fyrir öll \(x\) sem uppfylla \(a-\delta_1 < x<a+\delta_1\).
Eins þá fæst af \(\lim_{x\to a} h(x) = L\) að til er \(\delta_2\) þannig að \(L-\epsilon<g(x)<L+\epsilon\) fyrir öll \(x\) sem uppfylla \(a-\delta_2 < x<a+\delta_2\).
Setjum nú \(\delta = \min\{\delta_1,\delta_2\}\) og athugum að það þýðir að fyrir sérhvert \(x\) sem uppfyllir \(a-\delta < x < a+\delta\) uppfyllir einnig \(a-\delta_1 < x<a+\delta_1\) og \(a-\delta_2 < x<a+\delta_2\). Þá gefur \(f(x)\leq g(x)\leq h(x)\) að
Þar með er \(L-\epsilon < g(x) < L+\epsilon\) og þá höfum við sýnt að \(\lim_{x\to a} g(x) = L\).
2.3.3. Dæmi: Markgildi með sínus
Dæmi
Sýnið fram á eftirfarandi:
- \[\lim_{x\to 0} \sin\left(\frac 1x\right) \quad \text{er ekki til}\]
- \[\lim_{x\to 0} x\sin\left(\frac 1x\right) = 0\]
- \[\lim_{x \to 0} \frac{\sin(x)}{x} = 1\]
Lausn á lið 1
Sönnum þetta með mótsögn. Gerum ráð fyrir að til sé markgildi \(L\) þannig að fyrir sérhvert \(\epsilon >0\) er til \(\delta>0\) þannig að \(|x-0|<\delta\) hefur í för með sér að \(|\sin(1/x) - L|<\epsilon\). Til þess að þetta leiði til mótsagnar þurfum við að finna \(\epsilon>0\) sem er þannig að sama hversu lítið \(\delta>0\) er valið þá er alltaf til \(x\) þannig að \(|x-0|<\delta\) og
Veljum \(\epsilon = 0,5\). Ástæðan fyrir þessu vali er sú að þar sem \(\sin(1/x)\) sveiflast á milli \(-1\) og \(1\) þá er nóg að velja tölu sem er þannig að fallið sveiflist út fyrir bilið \([L-\epsilon,L+\epsilon]\). Í þessu tilviki þýðir það að \(\epsilon\) þarf að vera minna en 1.
Ef markgildið er til þá er ætti að vera til \(\delta>0\) þannig að \(|\sin(1/x)-L|< 0.5\) fyrir \(x\) sem uppfylla \(|x-0|<\delta\). Byrjum á að skoða tilvikið \(L\leq 0\). Finnum nógu stóra náttúrlega tölu \(k\) þannig að \(\frac 1{2\pi k + \pi/2} < \delta\). Ef við setjum \(x=\frac 1{2\pi k + \pi/2}\) þá fæst að \(|x-0|<\delta\) en
Tilvikið þegar \(L>0\) er eins nema þá veljum við \(x=\frac 1{2\pi k - \pi/2}\) sem þýðir að \(\sin(x) = -1\).
Mynd af \(\sin\left(\frac 1x\right)\):
2.4. Markgildi þegar x stefnir á óendanlegt

2.4.1. Óformleg skilgreining á markgildi þegar \(x \to \infty\)
Gerum ráð fyrir að fall \(f\) sé skilgreint á bili \((a, \infty)\). Segjum að \(f(x)\) stefni á tölu \(L\) þegar \(x\) stefnir á \(\infty\), og ritum \(\lim_{x\rightarrow \infty} f(x)=L\), ef við getum tryggt að \(f(x)\) sé eins nálægt \(L\) og við viljum bara með því að velja \(x\) nógu stórt.
2.4.2. Skilgreining: Markgildi þegar \(x \to \infty\)
Skilgreining
Gerum ráð fyrir að fall \(f\) sé skilgreint á bili \((a,\infty)\). Við segjum að \(f(x)\) stefni á tölu \(L\) þegar \(x\) stefnir á \(\infty\), og ritum \(\lim_{x\rightarrow \infty} f(x)=L\), ef eftirfarandi skilyrði er uppfyllt:
Fyrir sérhverja tölu \(\epsilon>0\) er til tala \(R\) þannig að um öll \(x>R\) gildir að
2.4.3. Óformleg skilgreining á markgildi þegar \(x \to -\infty\)
Fyrir \(-\infty\) er þetta gert með sama sniði.
Gerum ráð fyrir að fall \(f\) sé skilgreint á bili \((-\infty, a)\). Segjum að \(f(x)\) stefni á tölu \(L\) þegar \(x\) stefnir á \(-\infty\), og ritum \(\lim_{x\rightarrow -\infty} f(x)=L\), ef við getum tryggt að \(f(x)\) sé eins nálægt \(L\) og við viljum bara með því að velja \(x\) sem nógu stóra neikvæða tölu.
2.4.4. Skilgreining: Markgildi þegar \(x \to -\infty\)
Skilgreining
Gerum ráð fyrir að fall \(f\) sé skilgreint á bili \((-\infty,a)\). Við segjum að \(f(x)\) stefni á tölu \(L\) þegar \(x\) stefnir á \(-\infty\), og ritum \(\lim_{x\rightarrow -\infty} f(x)=L\), ef eftirfarandi skilyrði er uppfyllt:
Fyrir sérhverja tölu \(\epsilon>0\) er til tala \(R\) þannig að um öll \(x<R\) gildir að
2.5. Óendanlegt sem markgildi
2.5.1. Óformleg skilgreining á markgildinu \(\infty\)
Gerum ráð fyrir að fall \(f\) sé skilgreint á opnu bili umhverfis punktinn \(a\), nema hvað hugsanlega er \(f(a)\) ekki skilgreint. Segjum að \(f(x)\) stefni á \(\infty\) þegar \(x\) stefnir á \(a\), og ritum \(\lim_{x\rightarrow a} f(x)=\infty\), ef við getum tryggt að \(f(x)\) sé hversu stórt sem við viljum bara með því að velja \(x\) nógu nálægt \(a\).
2.5.2. Skilgreining: Markgildið \(\infty\)
Skilgreining
Gerum ráð fyrir að fall \(f\) sé skilgreint á opnu bili umhverfis punktinn \(a\), nema hvað hugsanlega er \(f(a)\) ekki skilgreint. Við segjum að \(f(x)\) stefni á \(\infty\) þegar \(x\) stefnir á \(a\), og ritum \(\lim_{x\rightarrow a} f(x)=\infty\), ef eftirfarandi skilyrði er uppfyllt.
Fyrir sérhverja tölu \(B\) er til tala \(\delta>0\) þannig að um öll \(x\) sem eru þannig að
Aðvörun
Athugið að \(\infty\) er ekki tala. Þó að \(\lim_{x\rightarrow a} f(x)=\infty\) þá er samt sagt að markgildið \(\lim_{x\rightarrow a} f(x)\) sé ekki til.
2.5.3. Óformleg skilgreining á markgildinu \(-\infty\)
Gerum ráð fyrir að fall \(f\) sé skilgreint á opnu bili umhverfis punktinn \(a\), nema hvað hugsanlega er \(f(a)\) ekki skilgreint. Segjum að \(f(x)\) stefni á \(-\infty\) þegar \(x\) stefnir á \(a\), og ritum \(\lim_{x\rightarrow a} f(x)=-\infty\), ef við getum tryggt að \(f(x)\) sé hversu lítið sem við viljum bara með því að velja \(x\) nógu nálægt \(a\).
2.5.4. Skilgreining: Markgildið \(-\infty\)
Skilgreining
Gerum ráð fyrir að fall \(f\) sé skilgreint á opnu bili umhverfis punktinn \(a\), nema hvað hugsanlega er \(f(a)\) ekki skilgreint. Við segjum að \(f(x)\) stefni á \(-\infty\) þegar \(x\) stefnir á \(a\), og ritum \(\lim_{x\rightarrow a} f(x)=-\infty\), ef eftirfarandi skilyrði er uppfyllt.
Fyrir sérhverja tölu \(B\) er til tala \(\delta>0\) þannig að um öll \(x\) sem eru þannig að
Aðvörun
Athugið að \(-\infty\) er ekki tala. Þó að \(\lim_{x\rightarrow a} f(x)=-\infty\) þá er samt sagt að markgildið \(\lim_{x\rightarrow a} f(x)\) sé ekki til.
2.5.5. Æfingadæmi
2.6. Samfelldni
Hér skilgreinum við og skoðum seinna grundvallarhugtakið í þessum kafla, sem er
samfelldni
en: continuity
Smelltu fyrir ítarlegri þýðingu.
2.6.1. Skilgreining: Innri punktur
Skilgreining
Látum \(A\subseteq {{\mathbb R}}\) og \(x\in A\). Við segjum að
\(x\) sé
innri punktur
en: inner point, interior point
Smelltu fyrir ítarlegri þýðingu.
Ef \(x\) er ekki innri punktur \(A\) og \(x\in A\) þá segjum
við að \(x\) sé
jaðarpunktur
en: boundary point, frontier point
Smelltu fyrir ítarlegri þýðingu.
2.6.2. Skilgreining: Samfelldni í punkti
Skilgreining
Látum \(f\) vera fall og \(c\) innri punkt skilgreiningarsvæðis \(f\). Sagt er að \(f\) sé samfellt í punktinum \(c\) ef
2.6.3. Setning
Setning
Látum \(f\) og \(g\) vera föll. Gerum ráð fyrir að \(c\) sé innri punktur skilgreiningarsvæðis beggja fallanna og að bæði föllin séu samfelld í punktinum \(c\). Þá eru eftirfarandi föll samfelld í \(c\):
\(f+g\)
\(f-g\)
\(fg\)
\(kf\), þar sem \(k\) er fasti
\(f/g\), ef \(g(c)\neq 0\)
\(\Big(f(x)\Big)^{1/n}\), að því gefnu að \(f(c)>0\) ef \(n\) er slétt tala og \(f(c)\neq 0\) ef \(n<0\).
Þessi setning er bein afleiðing af Setningu 2.3.1.
2.6.4. Setning: Samskeyting samfelldra falla
Setning
Látum \(g\) vera fall sem er skilgreint á opnu bili umhverfis \(c\) og samfellt í \(c\) og látum \(f\) vera fall sem er skilgreint á opnu bili umhverfis \(g(c)\) og samfellt í \(g(c)\). Þá er fallið \(f\circ g\) skilgreint á opnu bili umhverfis \(c\) og er samfellt í \(c\).
Athugasemd
Ef fall er skilgreint með formúlu og skilgreingamengið er ekki tilgreint sérstaklega, þá er venjan að líta alla þá punkta þar sem formúlan gildir sem skilgreingarmengi fallsins
2.6.5. Skilgreining: Samfellt fall
Skilgreining
Við segjum að fall \(f\) sé
samfellt
en: continuous function
Smelltu fyrir ítarlegri þýðingu.
Óformlega þýðir þetta að hægt er að teikna graf \(f\) án þess að lyfta pennanum frá blaðinu.
2.6.6. Nokkur dæmi um samfelld föll
Eftirfarandi föll eru samfelld
margliður
ræð föll
ræð veldi
hornaföll; \(\sin\), \(\cos\), \(\tan\)
tölugildisfallið \(|x|\)
2.6.7. Að búa til samfelld föll
Með því að nota föllin úr dæminu á undan sem efnivið þá getum við búið til fjölda samfelldra fall með því að beita aðgerðunum úr Setningu 2.6.4 og Setningu 2.6.3.
2.6.8. Dæmi
Fallið \(\cos(3x+5)\) er samfellt. Margliðan \(g(x) =3x+5\) og \(f(x) = \cos(x)\) eru samfelld föll og þá er samskeytingin \(f\circ g(x) = \cos(3x+5)\) einnig samfellt fall.
2.7. Hægri/vinstri samfelldni
Rifjum upp skilgreininguna á samfelldni.
2.7.1. Skilgreining
Skilgreining
Látum \(f\) vera fall og \(c\) innri punkt skilgreiningarsvæðis \(f\). Sagt er að \(f\) sé samfellt í punktinum \(c\) ef
Athugasemd
Þessi skilgreining virkar aðeins fyrir innri punkta skilgreiningarsvæðisins. Þannig að ef ætlunin er að rannsaka samfelldni í jaðarpunktum þá gengur þessi skilgreining ekki. Hins vegar getum við útvíkkað skilgreininguna á samfelldni fyrir hægri og vinstri endapunkta bila með því að einskorða okkur við markgildi frá vinstri og hægri.
2.7.2. Skilgreining: Hægri/vinstri samfelldni
Skilgreining
Fall \(f\) er samfellt frá hægri í punkti \(c\) ef \(\lim_{x\rightarrow c^+}f(x)=f(c)\).
Hér er gert ráð fyrir að fallið \(f\) sé amk. skilgreint á bili \([c, a)\).
Fall \(f\) er samfellt frá vinstri í punkti \(c\) ef \(\lim_{x\rightarrow c^-}f(x)=f(c)\).
Hér er gert ráð fyrir að fallið \(f\) sé amk. skilgreint á bili \((a, c]\).
Uppfærum nú skilgreininguna á samfelldu falli.
2.7.3. Uppfærð skilgreining: Samfellt fall
Skilgreining
Gerum ráð fyrir að \(f\) sé fall sem er skilgreint á mengi \(A\), þar sem \(A\) er sammengi endanlega margra bila. Við segjum að fallið \(f\) sé samfellt ef það er samfellt í öllum innri punktum skilgreingarmengisins og ef það er samfellt frá hægri/vinstri í jaðarpunktum skilgreingarmengisins, eftir því sem við á.
Athugasemd
Ef fall er samfellt á opnu bili \((a,b)\), og ef \(a<c<d<b\), þá er fallið einnig samfellt á bilinu \([c,d]\).
2.8. Eiginleikar samfelldra falla
2.8.1. Setning: Há- og lággildislögmálið
Há- og lággildislögmálið
Látum \(f\) vera samfellt fall skilgreint á lokuðu takmörkuðu bili \([a,b]\). Þá eru til tölur \(x_1\) og \(x_2\) í \([a,b]\) þannig að fyrir allar tölur \(x\) í \([a,b]\) er
Þetta þýðir að samfellt fall \(f\) á lokuðu og takmörkuðu bili \([a,b]\) tekur bæði hæsta og lægsta gildi á bilinu. Hæsta gildið er þá \(f(x_2)\) og lægsta gildið er \(f(x_1)\).
Athugasemd
Það er mögulegt að fallið taki há/lággildi sitt í fleiri en einum punkti.
2.8.2. Setning: Milligildissetningin
Milligildissetningin
Látum \(f\) vera samfellt fall skilgreint á lokuðu takmörkuðu bili \([a,b]\). Gerum ráð fyrir að \(s\) sé tala sem liggur á milli \(f(a)\) og \(f(b)\). Þá er til tala \(c\) sem liggur á milli \(a\) og \(b\) þannig að \(f(c)=s\).
Sönnun
Í setningunni þá gerum við ráð fyrir að \(s\) liggi á milli \(f(a)\) og \(f(b)\). Til að svona \(s\) sé til þá þarf \(f(a) \neq f(b)\).
Skoðum tilvikið þegar \(f(a) < f(b)\), en þá er \(f(a) < s < f(b)\). Tilvikið \(f(a)>f(b)\) er nánast eins.
Skilgreinum mengið \(S = \{ x \in [a,b] ; f(x) < s\}\). Þetta mengi er ekki tómt því \(a\) er í því og það er takmarkað að ofan af \(b\). Samkvæmt Frumsendunni um efra mark þá er til efra mark \(c \in[a,b]\) fyrir \(S\). Við viljum sýna að \(f(c)=s\).
Ef \(f(c)>s\) þá segir samfelldni \(f\) okkur að til sé lítið bil kringum \(c\) þar sem fallið er stærra en \(s\). Sér í lagi er til tala minni en \(c\) sem er ekki í menginu \(S\). Þetta þýðir að \(c\) er ekki efra mark \(S\). Orðum þetta aðeins nákvæmar.
Veljum \(0<\epsilon < f(c)-s\) þá er til \(\delta>0\) þannig að ef \(x\in ]c-\delta,c+\delta[\) þá er \(|f(c)-f(x)|<\epsilon < f(c) -s\). Þetta hefur í för með sér að \(f(c) - f(x) < f(c) -s\), það er \(f(x)>s\). Þetta þýðir að öll \(x\in]c-\delta,c[\) eru „minni“ efri mörk fyrir \(S\) en \(c\) sem gengur ekki og er því mótsögn.
Ef \(f(c)<s\) þá segir samfelldni \(f\) okkur að til sé lítið bil kringum \(c\) þar sem fallið er minna en \(s\). Sér í lagi er til tala stærri en \(c\) sem er í menginu \(S\). Þetta þýðir að \(c\) er ekki efra mark, því efra mark á að vera stærra eða jafnt og öll stök í \(S\). Þetta er einnig mótsögn.
Þá er bara eftir möguleikinn \(f(c)=s\), sem er nákvæmlega það sem við vildum.
Athugasemd
Það er möguleiki að það séu fleiri en einn punktur á bilinu þar sem fallið tekur gildið \(s\). Sönnunin hér á undan finnur þann stærsta.
2.8.3. Fylgisetning
Fylgisetning
Ef \(P(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0\) er margliða af oddatölu stigi \(n\), þá er til rauntala \(c\) þannig að \(P(c)=0\).
Sönnun
Gerum ráð fyrir að \(a_n>0\). Þá er \(\lim_{x\to -\infty} P(x) = -\infty\) og \(\lim_{x\to \infty} P(x) = \infty\). Það þýðir að til eru tölur \(a\) og \(b\) þannig að \(P(a)<0\) og \(P(b)>0\). Með því að beita Milligildissetningunni á fallið \(P\) á bilinu \([a,b]\) og með \(s=0\) þá fæst að til er núllstöð á bilinu \([a,b]\).
Ef \(a_n < 0\) þá víxlast formerkin á markgildunum hér að ofan en röksemdafærslan er að öðru leyti eins.