3. Útgildisverkefni

Old stories are like old friends, she used to say. You have to visit them from time to time.

-George R.R. Martin, A Storm of Swords

3.1. Útgildi

3.1.1. Skilgreining

Skilgreining

Látum $f$ vera fall af tveim breytum skilgreint á mengi ${\cal D}(f)$.

Sagt er að $f$ hafi staðbundið lággildi en: local minimum, minimum, minimum in the small, relative minimum
Smelltu fyrir ítarlegri þýðingu. í punkti $(a,b)$ ef til er tala $r>0$ þannig að $f(a,b)\leq f(x,y)$ fyrir alla punkta $(x,y)\in B_r(a,b)\cap{\cal D}(f)$.

Sagt er að $f$ hafi staðbundið hágildi en: local maximum, maximum, maximum in the small, relative maximum
Smelltu fyrir ítarlegri þýðingu. í punkti $(a,b)$ ef til er tala $r>0$ þannig að $f(a,b)\geq f(x,y)$ fyrir alla punkta $(x,y)\in B_r(a,b)\cap{\cal D}(f)$.

Í þeim punktum þar sem $f$ tekur annað hvort staðbundið lággildi eða staðbundið hágildi er sagt að $f$ hafi staðbundið útgildi en: extremum in the small, local extremum, relative extremum
Smelltu fyrir ítarlegri þýðingu.

Ef $f(a,b)\leq f(x,y)$ fyrir alla punkta $(x,y)\in {\cal D}(f)$ þá er sagt að $f$ taki lægsta gildi í $(a,b)$ (e. global minimum). Ef $f(a,b)\geq f(x,y)$ fyrir alla punkta $(x,y)\in {\cal D}(f)$ þá er sagt að $f$ taki hæsta gildi en: absolute maximum, global maximum, largest value, maximum in the large
Smelltu fyrir ítarlegri þýðingu. í $(a,b)$.

3.2. Staðbundið útgildi

3.2.1. Upprifjun

Látum $f$ vera fall af einni breytu skilgreint á mengi ${\cal D}(f)\subseteq {\mathbb R}$. Ef fallið $f$ hefur staðbundið útgildi í punkti $a$ þá gildir eitt af þrennu um $a$:

$f'(a)=0$. (punkturinn $a$ kallast stöðupunktur en: critical point, equilibrium point, extremal, singular point, stationary point, vanishing
Smelltu fyrir ítarlegri þýðingu.
$f$).
Afleiðan $f'(a)$ er ekki skilgreind.
Punkturinn $a$ er jaðarpunktur en: boundary point, frontier point
Smelltu fyrir ítarlegri þýðingu. ${\cal D}(f)$.

3.2.2. Setning

Setning

Látum $f$ vera fall af tveim breytum skilgreint á mengi ${\cal D}(f)\subseteq {\mathbb R}^2$. Ef fallið $f$ hefur staðbundið útgildi en: extremum in the small, local extremum, relative extremum
Smelltu fyrir ítarlegri þýðingu. í punkti $(a,b)$ þá gildir eitt af þrennu um $a$

$\nabla f(a,b)=\mbox{${\bf 0}$}$. (punkturinn $(a,b)$ kallast stöðupunktur en: critical point, equilibrium point, extremal, singular point, stationary point, vanishing
Smelltu fyrir ítarlegri þýðingu. $f$)
Stigullinn en: gradient
Smelltu fyrir ítarlegri þýðingu. $\nabla f(a,b)$ er ekki skilgreindur.
Punkturinn $(a,b)$ er jaðarpunktur en: boundary point, frontier point
Smelltu fyrir ítarlegri þýðingu. ${\cal D}(f)$.

3.2.3. Dæmi

Dæmi

Skoðum þrjú föll skilgreind á svæðinu $-0.5 \leq x \leq 0.5$, $-0.5 \leq y \leq 0.5$. Hvar eru staðbundin hágildi fallanna?

../_images/peak_smooth.png — Mynd 3.1 $z = f(x,y) = 1-x^2-y^2$.

../_images/peak.png — Mynd 3.2 $z = f(x,y) = 1-\sqrt{x^2+y^2}$.

../_images/max_bound.png — Mynd 3.3 $z= f(x,y) = x^2+y^2$.

3.3. Tilvist útgilda

3.3.1. Setning

Setning

Látum $f$ vera samfellt fall af tveim breytum skilgreint á lokuðu og takmörkuðu mengi ${\cal D}(f)$. Fallið $f$ tekur þá bæði hæsta og lægsta gildi.

3.4. Söðulpunktur

3.4.1. Skilgreining

Skilgreining

Punktur $(x,y)\in {\cal D}(f)$ sem er ekki jaðarpunktur kallast söðulpunktur en: saddle point
Smelltu fyrir ítarlegri þýðingu. ef $\nabla f(x,y)=\mbox{${\bf 0}$}$ en $f$ hefur ekki staðbundið útgildi í $(x,y)$.

Dæmi um föll með söðulpunkta.

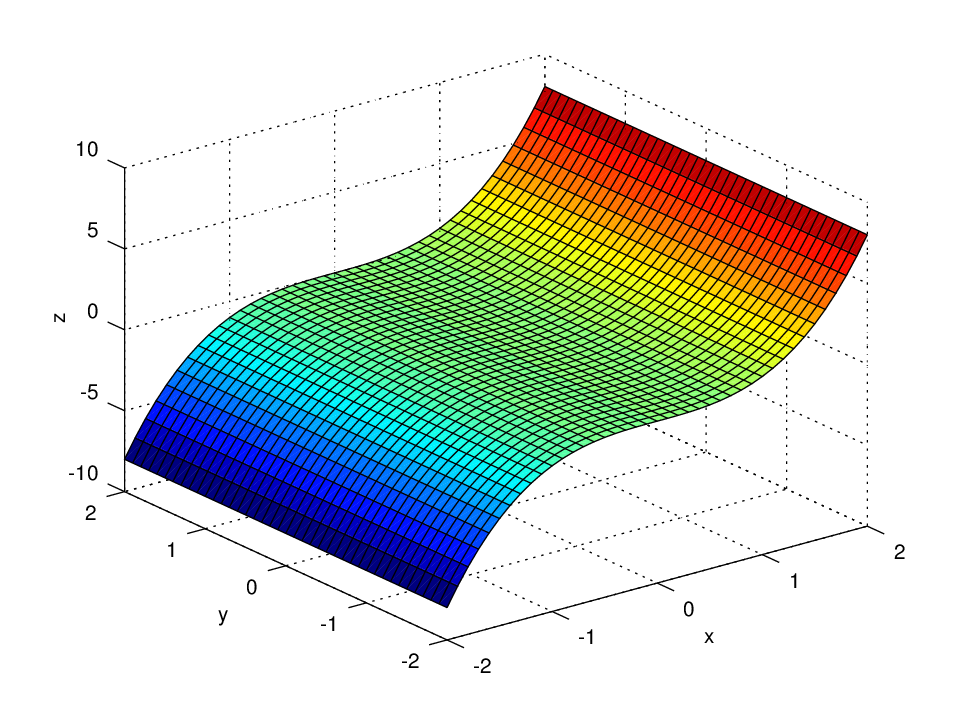
../_images/sodull1.png — Mynd 3.4 $z = f(x,y) = x^3$.

../_images/sodull2.png — Mynd 3.5 $z = f(x,y) = x^3+y^3$.

3.5. Staðbundið útgildi

3.5.1. Upprifjun

Látum $f$ vera fall af einni breytistærð og gerum ráð fyrir að $f'$ sé samfellt fall. Gerum einnig ráð fyrir að $f'(a)=0$. Þá gildir:

Ef $f''(a)>0$ þá hefur $f$ staðbundið lággildi en: local minimum, minimum, minimum in the small, relative minimum
Smelltu fyrir ítarlegri þýðingu. í $a$.
Ef $f''(a)<0$ þá hefur $f$ staðbundið hágildi en: local maximum, maximum, maximum in the small, relative maximum
Smelltu fyrir ítarlegri þýðingu. í $a$.
Ef $f''(a)=0$ þá gæti verið staðbundið lággildi í $A$, það gæti verið staðbundið hágildi í $a$ eða það gætu verið beygjuskil í $a$, alltsvo. ekkert hægt að segja.

3.6. Hesse-fylki

3.6.1. Skilgreining

Skilgreining

Látum $f$ vera fall af $n$ breytum $\mathbf{x} = (x_1,x_2,\ldots,x_n)$ og gerum ráð fyrir að allar 2. stigs hlutafleiður $f$ séu skilgreindar í punktinum $\mathbf{x}$. Skilgreinum Hesse-fylki $f$ í punktinum $\mathbf{x}$ sem $n\times n$-fylkið

\[\begin{split}{\cal H}(\mathbf{x})=\begin{bmatrix} f_{11}(\mathbf{x})&f_{12}(\mathbf{x}) & \cdots & f_{1n}(\mathbf{x})\\ f_{21}(\mathbf{x})&f_{22}(\mathbf{x}) & \cdots & f_{2n}(\mathbf{x}) \\ \vdots & \vdots & \ddots & \vdots & \\ f_{n1}(\mathbf{x})&f_{n2}(\mathbf{x}) & \cdots & f_{nn}(\mathbf{x})\end{bmatrix}.\end{split}\]

3.7. Ferningsform (sjá kafla 10.7 í Adams)

3.7.1. Upprifjun

Ferningsform en: quadratic form
Smelltu fyrir ítarlegri þýðingu. $Q$ af $n$-breytum $x_1,x_2,\ldots, x_n$ er einsleit margliða af stigi 2 gefin með

\[Q(\mathbf{x}) = \mathbf{x}^T A \mathbf{x}\]

þar sem $A$ er samhverft $n \times n$ fylki með tölu $a_{ij}$ í sæti $(i,j)$ og $\mathbf{x} = [x_1,x_2,\ldots x_n]^T$.

3.7.2. Skilgreining

Skilgreining

Ferningsform $Q$ af $n$-breytum er sagt vera jákvætt ákvarðað en: positive definite
Smelltu fyrir ítarlegri þýðingu. ef $Q(\mbox{${\bf x}$})>0$ fyrir alla vigra $\mbox{${\bf x}$}\neq \mbox{${\bf 0}$}$ í $\mbox{${\bf R}^n$}$.

Sagt að ferningsformið $Q$ sé neikvætt ákvarðað en: negative definite
Smelltu fyrir ítarlegri þýðingu. ef $Q(\mbox{${\bf x}$})<0$ fyrir alla vigra $\mbox{${\bf x}$}\neq \mbox{${\bf 0}$}$ í $\mbox{${\bf R}^n$}$.

Síðan er sagt að ferningsformið $Q$ sé óákvarðað en: undetermined
Smelltu fyrir ítarlegri þýðingu. ef $Q(\mbox{${\bf x}$})<0$ fyrir einhvern vigur $\mbox{${\bf x}$}$ og $Q(\mbox{${\bf y}$})>0$ fyrir einhvern vigur $\mbox{${\bf y}$}$.

3.7.3. Setning

Setning

Látum $Q$ vera fernings form af $n$ breytum og $A$ samhverft $n\times n$ fylki þannig að $Q(\mbox{${\bf x}$})=\mbox{${\bf x}$}^TA\mbox{${\bf x}$}$ fyrir alla vigra $\mbox{${\bf x}$}$,

Ferningsformið er jákvætt ákvarðað ef og aðeins ef öll eigingildi en: characteristic value, eigenvalue, proper value
Smelltu fyrir ítarlegri þýðingu. $A$ eru jákvæð.
Ferningsformið er neikvætt ákvarðað ef og aðeins ef öll eigingildi en: characteristic value, eigenvalue, proper value
Smelltu fyrir ítarlegri þýðingu. $A$ eru neikvæð.
Ferningsformið er óákvarðað ef og aðeins ef $A$ hefur bæði jákvæð og neikvæð eigingildi en: characteristic value, eigenvalue, proper value
Smelltu fyrir ítarlegri þýðingu.

3.8. Staðbundið útgildi

3.8.1. Setning

Setning

Látum $f$ vera fall af $n$ breytum $\mathbf{x} = (x_1,x_2,\ldots,x_n)$ þannig að allar 1. og 2. stigs hlutafleiður $f$ eru samfelldar. Látum $\mathbf{a}$ vera innri punkt á skilgreiningarsvæði $f$ og gerum ráð fyrir að $\nabla f(\mathbf{a})=\mbox{${\bf 0}$}$. Þá gildir: Ef ${\cal H}(\mathbf{a})$ er

…jákvætt ákvarðað þá hefur $f$ staðbundið lággildi en: local minimum, minimum, minimum in the small, relative minimum
Smelltu fyrir ítarlegri þýðingu. í $\mathbf{a}$.
…neikvætt ákvarðað þá hefur $f$ staðbundið hágildi en: local maximum, maximum, maximum in the small, relative maximum
Smelltu fyrir ítarlegri þýðingu. í $\mathbf{a}$.
…óákvarðað þá hefur $f$ söðulpunkt en: saddle point
Smelltu fyrir ítarlegri þýðingu. í $\mathbf{a}$.
…hvorki jákvætt ákvarðað, neikvætt ákvarðað né óákvarðað þá nægja upplýsingarnar sem felast í jöfnunni $\nabla f(\mathbf{a})=\mbox{${\bf 0}$}$ og Hesse-fylkinu ekki til að segja til um hvers eðlis stöðupunkturinn $\mathbf{a}$ er.

3.8.2. Fylgisetning

Setning

Látum $f$ vera fall af tveim breytum þannig að 1. og 2. stigs hlutafleiður $f$ eru samfelldar. Látum $(a,b)$ vera innri punkt á skilgreiningarsvæði $f$ og gerum ráð fyrir að $\nabla f(a,b)=\mbox{${\bf 0}$}$. Setjum

\[A=f_{11}(a,b),\qquad\quad B=f_{12}(a,b)=f_{21}(a,b)\qquad\quad C=f_{22}(a,b).\]

Þá gildir:

Ef $B^2-AC<0$ og $A>0$ þá hefur $f$ staðbundið lággildi en: local minimum, minimum, minimum in the small, relative minimum
Smelltu fyrir ítarlegri þýðingu. í $(a,b)$.
Ef $B^2-AC<0$ og $A<0$ þá hefur $f$ staðbundið hágildi en: local maximum, maximum, maximum in the small, relative maximum
Smelltu fyrir ítarlegri þýðingu. í $(a,b)$.
Ef $B^2-AC>0$ þá hefur $f$ söðulpunkt en: saddle point
Smelltu fyrir ítarlegri þýðingu. í $(a,b)$.
Ef $B^2-AC=0$ þá er ekkert hægt að segja.

3.9. Ferningsform

3.9.1. Regla

Setning

Ef $A$ er samhverft $n \times n$ fylki með tölu $a_{ij}$ í sæti $(i,j)$ og

\[\begin{split}D_i = \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1i} \\ a_{21} & a_{22} & \cdots & a_{2i} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{ii} \end{vmatrix}\end{split}\]

þá gildir

Ef $D_i > 0$ fyrir $1\leq i \leq n$ þá er $A$ jákvætt ákvarðað en: positive definite
Smelltu fyrir ítarlegri þýðingu. .
Ef $D_i > 0$ fyrir slétt $i$ í $\{1,2,\ldots,n\}$ og $D_i < 0$ fyrir oddatölu $i$ í $\{1,2,\ldots,n\}$ þá er $A$ neikvætt ákvarðað en: negative definite
Smelltu fyrir ítarlegri þýðingu. .
Ef $\det(A) = D_n \neq 0$ en hvorki $1$ né $2$ gilda þá er $A$ óákvarðað Ekki fannst þýðing á hugtakinu: óákvarðað .
Ef $\det(A) = 0$ þá er $A$ hvorki jákvætt né neikvætt ákvarðað en getur verið óákvarðað en: undetermined
Smelltu fyrir ítarlegri þýðingu. .

3.10. Útgildi falla þar sem breytur uppfylla skorðujöfnur

3.10.1. Sértækar aðferðir

Finna skal útgildi falls $f(x,y)$ þegar skilgreiningarsvæði $f$ er mengi þeirra punkta $(x,y)$ sem uppfylla jöfnu $g(x,y)=0$.

Er mögulegt að einangra $x$ eða $y$ í jöfnunni $g(x,y)=0$?
- Ef hægt er að einangra $y$ og rita $y=h(x)$ þá snýst verkefnið nú um að finna útgildi falls $f(x,h(x))$ af einni breytu $x$.
Er hægt að stika ferilinn $g(x,y)=0$?
- Ef $\mbox{${\bf r}$}$ er stikun á ferlinum þá þurfum við að leita að útgildum fallsins $f(\mbox{${\bf r}$}(t))$ þar sem er bara ein breyta.

3.10.2. Dæmi

Dæmi

Hver eru hæstu og lægstu gildi fallsins $f(x,y) = x^2-y^2+4$ á menginu $\{(x,y)~|~x^2+y^2=1\}$?

3.10.3. Setning

Setning

Látum $f$ og $g$ vera föll sem eru bæði diffranleg í punktinum $P_0=(x_0,y_0)$ sem liggur á ferlinum $g(x,y)=0$, og er ekki endapunktur ferilsins. Gerum ráð fyrir að $\nabla g(x_0,y_0)\neq \mbox{${\bf 0}$}$. Gerum líka ráð fyrir að ef við einskorðum fallið $f$ við ferilinn $g(x,y)=0$ þá hafi $f$ staðbundið útgildi í $P_0$. Þá eru stiglarnir $\nabla f(x_0,y_0)$ og $\nabla g(x_0,y_0)$ samsíða.

Ef stiglarnir $\nabla g(P_0)$ og $\nabla f(P_0)$ eru ekki samsíða þá vex $f$ eða minnkar þegar farið er eftir $\mathcal{C}$ út frá punktinum $P_0$.

3.11. Lagrange-margfaldarar

3.11.1. Reikniaðferð

Finna skal útgildi falls $f(x,y)$ þegar skilgreiningarsvæði $f$ er mengi þeirra punkta $(x,y)$ sem uppfylla jöfnu $g(x,y)=0$.

Búum til Lagrange-fallið

\[L(x,y,\lambda)=f(x,y)+\lambda g(x,y).\]

Stöðupunktar en: critical point, equilibrium point, extremal, singular point, stationary point, vanishing
Smelltu fyrir ítarlegri þýðingu. $L$, þ.e.a.s. punktar $(x_0,y_0,\lambda_0)$ þar sem $\nabla L(x_0,y_0,\lambda_0)=\mbox{${\bf 0}$}$, gefa mögulega punkta $(x_0,y_0)$ þar sem $f$ tekur útgildi.

Þessir punktar finnast með því að leysa jöfnuhneppið

\[\begin{split}\begin{aligned} f_1(x,y)+\lambda g_1(x,y)&=0\\ f_2(x,y)+\lambda g_2(x,y)&=0\\ g(x,y)&=0.\end{aligned}\end{split}\]

Talan $\lambda$ nefnist Lagrange-margfaldari.

3.11.2. Regla

Setning

Finna skal útgildi Ekki fannst þýðing á hugtakinu: útgildi falls $f(x,y)$ þegar skilgreiningarsvæði $f$ er mengi þeirra punkta $(x,y)$ sem uppfylla jöfnu $g(x,y)=0$.

Athuga þarf punkta sem uppfylla eitt af eftirfarandi skilyrðum:

Stöðupunktar en: critical point, equilibrium point, extremal, singular point, stationary point, vanishing
Smelltu fyrir ítarlegri þýðingu. $L(x,y,\lambda)$.
Punktar $(x,y)$ þar sem $\nabla g(x,y)=\mbox{${\bf 0}$}$
Punktar $(x,y)$ þar sem annar eða báðir stiglanna $\nabla g(x,y)$ og $\nabla f(x,y)$ eru ekki skilgreindir.
,,Endapunktar” ferilsins $g(x,y)=0$.

3.11.3. Reikniaðferð

Finna skal útgildi Ekki fannst þýðing á hugtakinu: útgildi falls $f(x,y,z)$ þegar skilgreiningarsvæði $f$ er mengi þeirra punkta $(x,y,z)$ sem uppfylla jöfnurnar $g(x,y,z)=0$ og $h(x,y,z)=0$.

Búum til Lagrange-fallið

\[L(x,y,z,\lambda,\mu)=f(x,y,z)+\lambda g(x,y,z)+\mu h(x,y,z).\]

Stöðupunktar en: critical point, equilibrium point, extremal, singular point, stationary point, vanishing
Smelltu fyrir ítarlegri þýðingu. $L$, þ.e.a.s. punktar $(x_0,y_0,z_0,\lambda_0,\mu_0)$ þar sem $\nabla L(x_0,y_0,z_0,\lambda_0,\mu_0)=\mbox{${\bf 0}$}$ gefa mögulega punkta $(x_0,y_0,z_0)$ þar sem $f$ tekur útgildi Ekki fannst þýðing á hugtakinu: útgildi .

Þessir punktar finnast með því að leysa jöfnuhneppið

\[\begin{split}\begin{aligned} f_1(x,y,z)+\lambda g_1(x,y,z)+\mu h_1(x,y,z)&=0\\ f_2(x,y,z)+\lambda g_2(x,y,z)+\mu h_2(x,y,z)&=0\\ f_3(x,y,z)+\lambda g_3(x,y,z)+\mu h_3(x,y,z)&=0\\ g(x,y,z)&=0\\ h(x,y,z)&=0.\end{aligned}\end{split}\]