6. Bútaaðferðir

Í þessum kafla fjöllum við um bútaaðferð en: finite element method
Smelltu fyrir ítarlegri þýðingu. . Eins og fyrir mismunaaðferðir eru til ólíkar útgáfur og við ætlum að skoða einföldustu tilfellin. Ennfremur, ætlum við að læra bútaaðferðir fyrir jaðargildisverkefni í \(\mathbb R\) og \(\mathbb{R}^2\).

6.1. Hlutheildun, innfeldi og tvílínulegt form

6.1.1. Jaðargildisverkefni í \(\mathbb R\)

Jaðargildisverkefnin í \(\mathbb R\) sem við viljum leysa eru

(6.1)\[\begin{split}\begin{cases} Lu=-(pu')'+qu=f,& \text{ á } ]a,b[,\\ B_1u=\alpha_1u(a)-\beta_1u'(a)=\gamma_1,&(\alpha_1,\beta_1)\neq (0,0),\\ B_2u=\alpha_2u(b)+\beta_2u'(b)=\gamma_2,&(\alpha_2,\beta_2)\neq (0,0). \end{cases}\end{split}\]

Þá er afleiðuvirkinn af Sturm-Liouville gerð, og við gerum ráð fyrir að \(p\) sé samfellt diffranlegt á bili \([a,b]\) og \(q\) sé samfellt á \([a,b]\).

Við skilgreinum \(V\) sem mengi raungildra falla sem eru samfelld og samfellt diffranleg á köflum á bilinu \([a,b]\), þ.e.a.s.

\[V=\{ \varphi: [a,b]\subset{\mathbb R}\to {{\mathbb R}}~; \varphi \in C[a,b]\cap PC^1[a,b] \}.\]

Athugum að

1. \(\varphi^\prime\) er heildanlegt fall á bilinu \([a,b]\) og undirstöðusetningin gildir í \(V\), þ.e.a.s.

\[\varphi(x)=\varphi(c)+\int_c^x\varphi'(t)\, dt, \qquad x,c\in [a,b],\]

af því að enda þótt \(\varphi\) sé ekki diffranlegt t.d. í \(x_\ell\), þá er \(\varphi\) í \(PC^1[a,b]\), þ.e.a.s. markgildi frá vinstri og hægri af afleiðunni \(\varphi^\prime\) eru til í \(x_\ell\),þ.e. \(\varphi^\prime(x_\ell+)\) og \(\varphi^\prime(x_\ell-)\) eru til og eru endanleg. Með öðrum orðum getum við alltaf skilgreint afleiðuna í \(x_\ell\) með

\[\varphi^\prime(x_\ell)=\tfrac 12\big(\varphi^\prime(x_\ell+)+\varphi^\prime(x_\ell-)\big).\]

2. Ennfremur gildir hlutheildun, þ.e. ef \(\varphi, \psi \in V\) þá er

\[-\int_c^d\psi'(x)\varphi(x)\, dx =\int_c^d\psi(x)\varphi'(x) \, dx -\big[\psi(x)\varphi(x)\big]_c^d \qquad c,d\in [a,b].\]

Munið að í 3.3.2 skilgreindum við

1. Innfeldi

Fyrir tvö raungild heildanleg föll \(\varphi\) og \(\psi\) á bilinu \([a,b]\), þá er innfeldi þeirra skilgreint með

\[{{\langle \varphi,\psi\rangle}}=\int_a^b \varphi(x)\psi(x)\, dx =\int_a^b \varphi \psi \, dx.\]

Ljóst er að innfeldi er vel skilgreint fyrir föllin í \(V\).

2. Tvílínulegt form sem \(L\) gefur af sér

Látum \(L\) vera afleiðuvirkja af Sturm-Liouville gerð. Við skilgreinum tvílínulega formið sem \(L\) gefur af sér með

\[{{\langle \varphi,\psi\rangle}}_L=\int_a^b\big(p\varphi' \psi' +q\varphi \psi\big)\, dx, \qquad \varphi, \psi \in V.\]

Nú ætlum við að nota þetta til þess að undirbúa nálgunarformúlur fyrir (6.1). Við tökum \(\varphi\in V\) og \(v\in \mathcal C^2([a,b])\) og við reiknum eftirfarandi innfeldi út

\[\begin{split}{{\langle Lv,\varphi\rangle}} &=& -\int_a^b {d\over dx}\left(p(x){dv\over dx} \right)\varphi dx+ \int_a^b q(x) v(x) \varphi(x) dx \\ &=& -\big[pv'\varphi\big]_a^b+ \int_a^b\big(pv'\varphi'+qv\varphi \big) \, dx.\end{split}\]

Við sjáum að það er

\[{{\langle Lv,\varphi\rangle}}={{\langle v,\varphi\rangle}}_L-\big[pv'\varphi\big]_a^b.\]

1. Ef við gerum ráð fyrir að \(\varphi\) uppfylli eftirfarandi jaðarskilyrði

\[\varphi(a)=\varphi(b)=0\]

þá verður innfeldið \(\langle Lv,\varphi\rangle\)

\[{{\langle Lv,\varphi\rangle}}={{\langle v,\varphi\rangle}}_L\,.\]

2. Ef við gerum ráð fyrir að \(v=u\) sé lausn á afleiðujöfnunni (6.1), þá er \(Lu=f\) og innfeldið verður

(6.2)\[{{\langle f,\varphi\rangle}}={{\langle u,\varphi\rangle}}_L, \qquad \varphi\in V, ~ \varphi(a)=\varphi(b)=0\,.\]

6.1.2. Jaðargildisverkefnin í \(\mathbb{R}^2\)

Við viljum halda áfram á svipaðan hátt í \(\mathbb{R}^2\). Nú er jaðargildisverkefnið í \(D\subset \mathbb{R}^2\)

(6.3)\[\begin{split}\begin{cases} Lu=-\nabla\cdot (p\nabla u)+qu=f, \qquad \text{ á } D,\\ \alpha u+\beta\dfrac{\partial u}{\partial n} =\gamma, \qquad \text{á } \ \partial D, \end{cases}\end{split}\]

og \(p\in C^1(D)\), \(q\) of \(f\) eru samfelld á \(D\). Athugum að \(p, q, f\) eru föll á \(D\subset \mathbb{R}^2\), og \(\gamma, \alpha, \beta\) eru föll á \(\partial D\subset \mathbb{R}^2\).

Athugum

1. Leibniz reglan í \(\mathbb{R}^n\)

\[\nabla\cdot \big(\varphi p\nabla u\big)= \big(\nabla\cdot(p\nabla u)\big)\varphi +p\nabla u \cdot \nabla \varphi,\]

af því að

\[\nabla\cdot (\varphi {\mathbf V})=(\nabla\cdot {\mathbf V})\varphi + {\mathbf V} \cdot \nabla \varphi,\]

og hér \(\mathbf V= p\nabla u\).

2. Gauss setning

\[\iint_D \nabla \cdot (\varphi p\nabla u)\, dA =\int_{\partial D} p\dfrac{\partial u}{\partial n}\varphi \, ds\]

3. Hlutheildun í \(\mathbb{R}^2\)

Við sjáum að úr 1. og 2. fáum við

\[-\iint\limits_D\nabla\cdot \big( p\nabla u\big) \varphi \, dA= -\int\limits_{\partial D} p\dfrac{\partial u}{\partial n}\varphi\, ds +\iint\limits_D p\nabla u\cdot \nabla \varphi\, dA.\]

Munið að

1. Innfeldi

Gerum ráð fyrir að \(\varphi\) og \(\psi\) séu tvö raungild heildanleg föll á \(\bar D= D \cap \partial D\), þá er innfeldi þeirra

\[{{\langle \varphi,\psi\rangle}}= \iint_D \varphi(x,y)\psi(x,y)\, dxdy =\iint_D \varphi\psi \, dA.\]

2. Tvílínulegt form sem \(L\) gefur af sér

Látum \(L\) vera hlutafleiðuvirkja eins og í verkefninu (6.1), og gerum ráð fyrir að \(\varphi\) og \(\psi\) séu þ.a. fyrsta stigs hlutafleiður þeirra séu vel skilgreindar og takmarkaðar á \(D\). Þá skilgreinum við tvílínulega formið með

\[{{\langle \varphi,\psi\rangle}}_L=\iint\limits_D\big(p\, \nabla \varphi\cdot \nabla \psi +q\, \varphi\psi\big)\, dA.\]

Við skoðum nú innfeldi milli \(Lv\) og \(\phi\), þar sem \(L\) er virkinn í (6.3). Við gerum ráð fyrir að \(v\in C^2(\overline D)\). Þá er

\[\begin{split}\begin{aligned} \langle L v, \varphi\rangle=\iint_D \big(Lv\big) \varphi\, dA &=\iint_D\big( p\, \nabla v\cdot \nabla \varphi+q v\varphi\big) \, dA-\int_{\partial D}p\dfrac{\partial v}{\partial n} \varphi \, ds\\ &={{\langle v,\varphi\rangle}}_L -\int_{\partial D}p\dfrac{\partial v}{\partial n} \varphi \, ds.\end{aligned}\end{split}\]

Við sjáum að

1. Ef \(\varphi\) er núll á jaðrinum \(\partial D\), þá er

\[\langle L v, \varphi\rangle={{\langle v,\varphi\rangle}}_L\]

2. Ef \(v=u\) er lausn á jaðarverkefni (6.3), þá gildir

(6.4)\[{{\langle u,\varphi\rangle}}_L={{\langle f,\varphi\rangle}}, \qquad \varphi\in C^1(\overline D), \quad \varphi=0 \text{ á } \partial D.\]

6.2. Aðferð Galerkins fyrir Dirichlet-verkefnið

6.2.1. Galerkin-aðferðir í einni vídd fyrir Dirichlet-verkefni

Við lítum á jaðargildisverkefnið (6.1) í sértilfellinu þegar \(\beta_1 =\beta_2=0\), þ.e.a.s. við höfum Dirichlet-verkefni:

(6.5)\[\begin{split}\begin{cases} Lu=-(pu')'+qu=f,& \text{ á } ]a,b[,\\ u(a)=\gamma_1/\alpha_1, \quad u(b)=\gamma_2/\alpha_2. \end{cases}\end{split}\]

Aðalatriðið í Galerkin-aðferð er að smíða nálgunarfall \(v(x)\) fyrir lausn \(u\) á Dirichlet-verkefninu að ofan á eftirfarandi hátt

\[v(x)=\psi_0(x)+c_1\varphi_1(x)+\cdots+c_N\varphi_N(x),\]

þar sem

1. fallið \(\psi_0(x)\) er valið þ.a. það uppfyllir jaðarskilyrðin í (6.5), þ.e.a.s.

\[\psi_0(a)=\gamma_1/\alpha_1, \qquad \psi_0(b)=\gamma_2/\alpha_2,\]

2. föllin \(\varphi_1,\dots,\varphi_N\) eru valin þ.a. þau uppfylla óhliðruðu jaðarskilyrðin, þ.e.a.s.

\[\varphi_j(a)=\varphi_j(b)=0, \qquad j=1, \dots, N,\]

3. stuðlanir \(c_1, \dots, c_N\) eru óþekktir, og markmiðið er að reikna þá út.

Það er ljóst að nálgunarfallið \(v\) uppfyllir jaðarskilyrðin í (6.5) by construction, þ.e.a.s.

\[v(a)=\gamma_1/\alpha_1, \qquad v(b)=\gamma_2/\alpha_2.\]

Hvernig getum við fundið nálgunargildi \(c_1, \dots, c_N\)? Við krefjumst að \(v\) uppfylli jöfnu (6.2), þá er

\[{{\langle v,\varphi_j\rangle}}_L={{\langle f,\varphi_j\rangle}}, \qquad j=1,2,\dots,N.\]

Við sjáum að þetta er jafngilt því að

\[{{\langle \psi_0,\varphi_j\rangle}}_L+\sum_{k=1}^Nc_k{{\langle \varphi_k,\varphi_j\rangle}}_L ={{\langle f,\varphi_j\rangle}}, \qquad j=1,\dots,N.\]

Nú höfum við \(N\times N\) jöfnuhneppi fyrir \(N\) nálgunargildi, af því að

(6.6)\[\begin{split}\begin{bmatrix} \langle \varphi_1, \varphi_1\rangle_L & \langle \varphi_1, \varphi_2\rangle_L & \dots &\langle \varphi_1, \varphi_N\rangle_L \\ \langle \varphi_2, \varphi_1\rangle_L & \langle \varphi_2, \varphi_2\rangle_L & \dots &\langle \varphi_2, \varphi_N\rangle_L \\ \vdots & \vdots &\ddots &\vdots \\ \langle \varphi_N, \varphi_1\rangle_L & \langle \varphi_N, \varphi_2\rangle_L & \dots & \langle \varphi_N, \varphi_N\rangle_L \end{bmatrix} \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\c_N \end{bmatrix} = \begin{bmatrix} -\langle \psi_0, \varphi_1\rangle_L +\langle f, \varphi_1\rangle \\ -\langle \psi_0, \varphi_2\rangle_L +\langle f, \varphi_2\rangle\\ \vdots \\ -\langle \psi_0, \varphi_N\rangle_L +\langle f,\varphi_N\rangle \end{bmatrix}.\end{split}\]

Almennt, ef afleiðuvirki er línulegur, þá er hneppið að ofan línulegt.

Þýðing og sambandið við jaðargildisverkefnin

Við sjáum að hugmyndin að baki aðferð Galerkins er frekar ólik m.v. mismunaaðferð. Í mismunaaðferðum fáum við algebrujöfnuhneppi úr afleiðujöfnum með því að nálga afleiður með mismunakvótum. Hér fáum við algebrujöfnuhneppi með því þess að krefjast þess að nálgunarfall uppfylli veika framsetningu afleiðujöfnunnar, sem er (6.2).

Munið að \({{\langle v,\varphi_j\rangle}}_L=\langle L v, \varphi_j\rangle\), þá segir jafnan (6.2) okkur að

\[{{\langle (L v-f),\varphi_j\rangle}}=0.\]

Ef \(u\) er nákvæm lausn á jöfnunni (6.5), það þýðir að \(Lu=f\), svo \((L v-f)\) er mismunur milli nálgunarfallsins \(v\) og lausnarinnar \(u\), og við krefjumst þess að mismunur þeirra sé þverstæður m.t.t. fallanna \(\varphi_j\) sem við notum til þess að smiða nálgunarfallið \(v\).

Af hverju? Aðalatriðið er að mismunurinn er lágmarkaður ef hann er þverstæður m.t.t. plansins sem er spannað af \(\varphi_j, ~j=1, \dots, N\), þ.e.

\[{{\langle L(v-u),\varphi_j\rangle}}=0.\]

Athugasemd

Föllin \(\varphi_j~j=1, \dots, N\) þurfa að vera línulega óháð! Annars hefur fylkið í (6.6) ekki max stétt!

6.2.2. Galerkin-aðferðir í tveimur víddum fyrir Dirichlet-verkefni

Við lítum á jaðargildisverkefnið (6.3) í sértilfellinu þegar \(\beta_1 =\beta_2=0\) á \(\partial D\), þ.e

(6.7)\[\begin{split}\begin{cases} Lu=-\nabla\cdot (p\nabla u)+qu=f, \qquad \text{ á } D,\\ u=\gamma/\alpha, \qquad \text{á } \ \partial D. \end{cases}\end{split}\]

Við höldum áfram á svipaðan hátt, og við skilgreinum nálgunarfall \(v\)

\[v(x,y)=\psi_0(x,y)+c_1\varphi_1(x,y)+\cdots+c_N\varphi_N(x,y), (x,y) \in \bar D,\]

þ.a.

1. fall \(\psi_0(x,y)\) uppfyllir eftirfarandi jaðarskilyrði

\[\psi_0(x,y)=\gamma(x,y)/\alpha(x,y), \qquad (x,y) \in \partial D\]

2. föllin \(\phi_j~j=1, \dots, N\) uppfylla eftirfarandi jaðarskilyrði

\[\varphi_j(x,y)=0, \qquad (x,y) \in \partial D, \qquad j=1, \dots, N,\]

Það er ljóst að nálgunarfallið uppfyllir a.m.k. jaðarskilyrðin í (6.7). Eins og áður er markmiðið að reikna stuðlana \(c_j\), og til þess að ákvarða þá notum við skilyrði (6.4),

\[\langle v, \varphi_j\rangle_L = \langle f , \varphi_j\rangle \,, \qquad j=1, \dots, N,\]

sem gefur okkur \(N\) skilyrði fyrir \(c_j\)

\[{{\langle \psi_0,\varphi_j\rangle}}_L+\sum_{k=1}^Nc_k{{\langle \varphi_k,\varphi_j\rangle}}_L ={{\langle f,\varphi_j\rangle}}, \qquad j=1,\dots,N.\]

Eins og áður getum við skrifað \(N \times N\) hneppi, þ.a. \([A]\vec{c} =\vec{b}\), þar sem

\[A_{jk}={{\langle \varphi_k,\varphi_j\rangle}}_L ={{\langle \varphi_j,\varphi_k\rangle}}_L, \qquad j,k=1,\dots,N,\]

og

\[b_j={{\langle f,\varphi_j\rangle}}-{{\langle \psi_0,\varphi_j\rangle}}_L, \qquad j=1,\dots,N.\]

Formlega höfum við sömu hneppi eins og í \(\mathbb R\). En nú erum við í \(\mathbb{R}^2\), þ.e.a.s. innfeldið og tvílínulega formið innihalda tvöfalt heildi (yfir \(x, y\)), sjáið 6.1.2.

6.3. Bútaaðferð í einni vídd

Hér beinum við athygli okkar að jaðargildisverkefni í einni vídd þar sem við veljum þúfugrunnföllin til þess að nálga lausn.

Almennt er jaðargildisverkefnið gefið með (6.1). Við veljum skiptingu á bili \([a,b]\), þ.e.

\[a=x_0<x_1<\cdots<x_N=b, ~~~ h:= (b-a)/N, ~~ x_j= a+j h, ~~j=0, \dots, N.\]

Munið líka að miðpunktar eru gefnir með

\[m_j= x_j+ h,~~~~j=0, \dots, N-1.\]

Munið að þúfugrunnföllin eru skilgreind þ.a. \(\varphi_j(x_i)=\delta_{ij}\), sjáið 5.2.2. Sérstaklega, þýðir það að þúfugrunnföllin eru í \(V\), og að \(\varphi_0(a)=1\) og \(\varphi_N(b)=1\).

6.3.1. Blönduð jaðarskilyrði í báðum endapunktum

Við gerum ráð fyrir að \(\beta_1\neq 0\) og \(\beta_2\neq 0\).

Við skilgreinum nálgunarfallið

\[v(x)=c_0\varphi_0(x)+\cdots+c_N\varphi_N(x).\]

Munið kafla 6.1.2, almennt höfum við

(6.8)\[{{\langle u,\varphi\rangle}}_L + p(a)u'(a)\varphi(a)-p(b)u'(b)\varphi(b) = {{\langle f,\varphi\rangle}}, \qquad \varphi\in V.\]

Við sjáum núna að \(\varphi(a), \varphi(b)\) eru ekki núll almennt, svo við þurfum að skoða jaðarliði líka. Fyrst notum við jaðarskilyrði í (6.1), þá fáum við

\[{{\langle u,\varphi\rangle}}_L + \dfrac {p(a)}{\beta_1}(\alpha_1u(a)-\gamma_1)\varphi(a) +\dfrac{p(b)}{\beta_2}(\alpha_2u(b)-\gamma_2)\varphi(b) ={{\langle f,\varphi\rangle}}.\]

Nú stingum við í jöfnuna að nálgunarfallið er gefið með samantekt af þúfugrunnföllum og notum \(\varphi_j\) í staðinn fyrir \(\varphi\). Þá er fyrir \(j=0, \dots, N\)

\[\sum_{i=0}^N c_i{{\langle \varphi_i ,\varphi_j\rangle}}_L + \dfrac {p(a)}{\beta_1}(\alpha_1 \sum_{i=0}^N c_i \varphi_i(a)-\gamma_1)\varphi_j(a) +\dfrac{p(b)}{\beta_2}(\alpha_2\sum_{i=0}^N c_i \varphi_i(b)-\gamma_2)\varphi_j(b) ={{\langle f,\varphi_j\rangle}}.\]

Það er gagnlegt að skrifa nálgunarformúlur á fylkjaformi, þ.e.a.s.

\[A{\mathbf c}={\mathbf b}, ~~~\text{þar sem}~~~ A=\big(a_{jk}\big)_{j,k=0}^N.\]

Stök fylkisins \(A\) eru gefin með

\[a_{ji}= {{\langle \varphi_i ,\varphi_j\rangle}}_L+ \dfrac {p(a)\alpha_1}{\beta_1}\varphi_i(a)\varphi_j(a)+\dfrac {p(b)\alpha_2}{\beta_2}\varphi_i(b)\varphi_j(b),~~~i,j=0, \dots, N,\]

og stuðlar vigursins \(\mathbf b\) eru gefnir með

\[b_j ={{\langle f,\varphi_j\rangle}}+\dfrac {p(a)\gamma_1}{\beta_1}\varphi_j(a) +\dfrac{p(b)\gamma_2}{\beta_2}\varphi_j(b), ~~~j=0, \dots, N.\]

Við viljum skoða jöfnuhneppið nánar. Munið

T.d. fyrir \(j=0\) þurfum við bara að reikna eftirfarandi stök

\[\begin{split}\begin{aligned} a_{00}&=\int_{x_0}^{x_1}\big(p(\varphi_0')^2+q\varphi_0^2\big)\, dx+ \dfrac{p(a)\alpha_1}{\beta_1} \\ a_{01}&= \int_{x_0}^{x_1}\big(p\varphi_0'\varphi_1'+q\varphi_0\varphi_1\big)\, dx \end{aligned}\end{split}\]

af því að \(\varphi_0\) hefur stoð á bili \([x_0,x_1]\), \(\varphi_j\) með \(j=1, \dots, N-1\) er ekki núll bara yfir bilið \([x_{j-1},x_{j+1}]\) og \(\varphi_N\) er ekki núll á bili \([x_{N-1},x_{N}]\).

Lítum nú a stuðla hægri hliðarinnar, þá er

\[b_0=\int_{x_0}^{x_1}f\varphi_0\, dx+\dfrac{p(a)\gamma_1}{\beta_1} \approx \dfrac{h f(m_0)}2+\dfrac{p(a)\gamma_1}{\beta_1},\]

af því að \(\varphi_0(a)=1\) og \(\varphi_0(b)=0\).

Nú viljum við nálga heildið að ofan, við getum haldið áfram eins og áður, t.d.

\[\begin{split}\begin{aligned} a_{00}&=\int_{x_0}^{x_1}\big(p(\varphi_0')^2+q\varphi_0^2\big)\, dx+ \dfrac{p(a)\alpha_1}{\beta_1} \approx \dfrac{p(m_0)}{h}+\dfrac{h q(m_0)}3+\dfrac{p(a)\alpha_1}{\beta_1} \\ a_{01}&= \int_{x_0}^{x_1}\big(p\varphi_0'\varphi_1'+q\varphi_0\varphi_1\big)\, dx \approx -\dfrac{p(m_0)}{h}+\dfrac{h q(m_0)}6. \\ b_0&=\int_{x_0}^{x_1}f\varphi_0\, dx+\dfrac{p(a)\gamma_1}{\beta_1} \approx \dfrac{h f(m_0)}6+\dfrac{p(a)\gamma_1}{\beta_1}.\end{aligned}\end{split}\]

Fyrir \(j=1, \dots, N-1\) þurfum við að reikna stökin \(a_{jj-1},a_{jj},a_{jj+1}\) og líka \(\mathbf{b}_j\). Við notum sömu nálgun fyrir heildið, þá er

\[\begin{split}\begin{aligned} a_{j,j-1}&=\int_{x_{j-1}}^{x_j} \big( p\varphi_{j-1}'\varphi_j'+q\varphi_{j-1}\varphi_j\big)\, dx \approx -\dfrac{p(m_{j-1})}{h}+\dfrac{h q(m_{j-1})}6,\\ a_{j,j}&=\int_{x_{j-1}}^{x_{j+1}} \big( p(\varphi_j')^2+q \varphi_j^2\big)\, dx \approx \dfrac{p(m_{j-1})}{h}+\dfrac{p(m_j)}{h} +\dfrac{(q(m_{j-1})+ q(m_j))h}3,\\ a_{j,j+1}&=\int_{x_j}^{x_{j+1}} \big( p\varphi_j'\varphi_{j+1}'+q \varphi_j\varphi_{j+1}\big)\, dx \approx -\dfrac{p(m_j)}{h} +\dfrac{h q(m_j)}6,\\ b_j&=\int_{x_{j-1}}^{x_{j+1}}f\varphi_j\, dx \approx \dfrac{h (f(m_{j-1})+f(m_j))}2.\end{aligned}\end{split}\]

Að lokum þurfum við að skoða \(j=N\), nú höfum við að \(\varphi_N(b)=1\), þá fáum við

\[\begin{split}\begin{aligned} a_{N,N-1}&=\int_{x_{N-1}}^{x_N} \big( p\varphi_{N-1}'\varphi_N'+q\varphi_{N-1}\varphi_N\big)\, dx \approx -\dfrac{p(m_{N-1})}{h}+\dfrac{h q(m_{N-1})}6,\\ a_{NN}&=\int_{x_{N-1}}^{x_{N}} \big( p\big(\varphi_N'\big)^2+q\varphi_N^2\big)\, dx +\dfrac{p(b)\alpha_2}{\beta_2} \approx \dfrac{p(m_{N-1})}{h} +\dfrac{h q(m_{N-1})}3+\dfrac{p(b)\alpha_2}{\beta_2},\\ b_N&=\int_{x_{N-1}}^{x_{N}}f\varphi_N\, dx+\dfrac{p(b)\gamma_2}{\beta_2} \approx \dfrac{h f(m_{N-1})}2+\dfrac{p(b)\gamma_2}{\beta_2}.\end{aligned}\end{split}\]

6.3.2. Fallsjaðarskilyrði

Lítum á jaðargildisverkefnið (6.1).

Við gerum ráð fyrir að \(\beta_1=0\), þ.e.a.s. að við höfum Dirchlet jaðarskilyrði í vinstri endapunktinum, þ.e. \(u(a)=\gamma_1/\alpha_1\).

Þá setjum við \(c_0=\gamma_1/\alpha_1\), svo að nálgunarfallið \(v\) tekur gildi \(\gamma_1/\alpha_1\) í punktinum \(a\). Það þýðir að fyrir \(j=0\) setjum við

\[a_{00}=1, \quad a_{0j}=0, \ j=1,\dots,N, \ b_0=\gamma_1/\alpha_1,\]

og jöfnuhneppið er eins og áður.

Ef við höfum Dirchlet jaðarskilyrði í hægri endapunktinum, þ.e.a.s. að \(\beta_2=0\), þá veljum við \(c_N=\gamma_2/\alpha_2\), svo að nálgunarfallið uppfyllir rétt jaðarskilyrði í \(b\). Þess vegna setjum við

\[a_{NN}=1, \quad a_{Nj}=0, \ j=0,\dots,N-1, \ b_N=\gamma_2/\alpha_2.\]

6.4. Aðferð Galerkins með almennum jaðarskilyrðum

Við lítum á jaðargildisverkefnið (6.1) og (6.3). Hér viljum við ekki tilgreina grunn fyrir nálgunarfall, en ætlum frekar að ákvarða skilyrði og nálgunarformúlur almennt.

Við skilgreinum veika framsetningu á jaðargildisverkefnunum með formúlu

(6.9)\[{{\langle u,\varphi\rangle}}_{L,B}={{\langle f,\varphi\rangle}}+T_B(\varphi), \qquad \varphi\in V_B,\]

þar sem

1. \((\psi,\varphi)\mapsto {{\langle \psi,\varphi\rangle}}_{L,B}\) er tvílínulegt form sem er bæði háð virkjanum \(L\) og jaðarskilyrðunum \(B\),

2. \(\varphi\mapsto T_B(\varphi)\) er línulegt form sem er háð jaðarskilyrðunum \(B\),

3. \(V_B\) er mengi af föllum, sem skilgreint er út frá jaðarskilyrðunum.

Við veljum \(\psi_0\) þ.a. fallið uppfylli viðeigandi jaðarskilyrði, og eftir það veljum við \(\varphi_1,\dots,\varphi_N\in V_B\) og krefjumst þess að nálgunarfallið \(v=\psi_0+c_1\varphi_1+\cdots+\varphi_N\) uppfylli línulega jöfnuhneppið (6.9).

Þá er almennt

\[{{\langle v,\varphi_j\rangle}}_{L,B}={{\langle f,\varphi_j\rangle}}+T_B(\varphi_j), \qquad j=1,\dots,N.\]

Á fylkjaformi höfum við

\[\begin{split}a_{jk} &=&{{\langle \varphi_k,\varphi_j\rangle}}_{L,B} ={{\langle \varphi_j,\varphi_k\rangle}}_{L,B}, \qquad j,k=1,\dots,N,\\ b_j &=& {{\langle f,\varphi_j\rangle}}+T_B(\varphi_j)-{{\langle \psi_0,\varphi_j\rangle}}_{L,B}, \qquad j=1,\dots,N,\end{split}\]

sem gefur okkur jöfnuhneppið á fylkjaformi:

\[A{\mathbf c}={\mathbf b}, ~~~\text{þar sem}~~~ A=\big(a_{jk}\big)_{j,k=1}^N.\]

Þá höfum við \(N\) algebrujöfnur fyrir \(N\) nálgunargildi \(c_j, ~j=1, \dots, N\), og við getum reiknað þau út.

6.4.1. Í einni vídd

Við skoðum nú (6.9) í ólíkum tilfellum. Munið samkvæmt kafla 6.1.2, höfum við almennt

(6.10)\[{{\langle u,\varphi\rangle}}_L + p(a)u'(a)\varphi(a)-p(b)u'(b)\varphi(b) = {{\langle f,\varphi\rangle}}, \qquad \varphi\in V.\]

1. Dirichlet-jaðarskilyrði

Þá er verkefnið eins og (6.5) sem við fjölluðum um í 6.2.1. Þá veljum við \(\psi_0\) þ.a. \(\psi_0(a)=\gamma_1/\alpha_1\) og \(\psi_0(b)=\gamma_2/\alpha_2\).

Hér skilgreinum við mengi falla

\[V_B=\{\varphi\in V\,;\, \varphi(a)=\varphi(b)=0\},\]

og þá er

\[{{\langle u,\varphi\rangle}}_L={{\langle f,\varphi\rangle}},\]

sem segir okkur að

\[{{\langle \varphi,\psi\rangle}}_{L,B}={{\langle \varphi,\psi\rangle}}_L ~~~\text{og}~~~ T_B(\varphi)=0 ~~~ \varphi,\psi\in V_B.\]

2. Dirichlet jaðarskilyrði í vinstri endapunkti

Lítum á

\[\begin{split}\begin{cases} Lu=-(pu')'+qu=f, \\ B_1u=\alpha_1u(a)=\gamma_1, \\ B_2u=\alpha_2u(b)+{\beta}_2u'(b)=\gamma_2, \quad \beta_2\neq 0. \end{cases}\end{split}\]

Nú tökum við

\[V_B=\{\varphi\in V\,;\, \varphi(a)=0\},\]

og notum jaðarskilyrði í hægri endapunkti til þess að einfalda tvílínulega formið (6.10), þ.e.a.s.

\[{{\langle u,\varphi\rangle}}_L +\dfrac{p(b)\alpha_2}{\beta_2}u(b)\varphi(b) ={{\langle f,\varphi\rangle}} +\dfrac{p(b)\gamma_2}{\beta_2}\varphi(b), ~~~ \varphi\in V_B.\]

Ef við berum jöfnuna að ofan saman við jöfnu (6.9), sjáum við að

\[{{\langle \varphi,\psi\rangle}}_{L,B}={{\langle \varphi,\psi\rangle}}_L +\dfrac{p(b)\alpha_2}{\beta_2}\varphi(b)\psi(b), \quad \text{ og } \quad T_B(\varphi)= \dfrac{p(b)\gamma_2}{\beta_2}\varphi(b), \qquad \varphi,\psi\in V_B.\]

3. Dirichlet jaðarskilyrði í hægri endapunkti

Lítum á

\[\begin{split}\begin{cases} Lu=-(pu')'+qu=f, \\ B_1u={\alpha}_1u(a)-\beta_1u'(a)=\gamma_1, \quad \beta_1\neq 0 \\ B_2u=\alpha_2u(b)=\gamma_2, \end{cases}\end{split}\]

og höldum áfram eins og áður. Við skilgreinum

\[V_B=\{\varphi\in V \,;\, \varphi(b)=0 \},\]

og með því að nota jaðarskilyrði verður formið (6.10)

\[{{\langle u,\varphi\rangle}}_L +\dfrac {p(a)\alpha_1}{\beta_1}u(a)\varphi(a) ={{\langle f,\varphi\rangle}} +\dfrac {p(a)\gamma_1}{\beta_1}\varphi(a), \qquad \varphi\in V_B.\]

Á svipaðan hátt berum við jöfnuna að ofan saman við (6.9), og sjáum að hér gildir

\[{{\langle \varphi,\psi\rangle}}_{L,B}={{\langle \varphi,\psi\rangle}}_L +\dfrac {p(a)\alpha_1}{\beta_1}\varphi(a)\psi(a) \quad \text{ og } \quad T_B(\varphi)=\dfrac {p(a)\gamma_1}{\beta_1}\varphi(a), \qquad \varphi,\psi\in V_B.\]

4. Blönduð jaðarskilyrði í báðum endapunktum

Jaðargildisverkefnið er

\[\begin{split}\begin{cases} Lu=-(pu')'+qu=f, \\ B_1u={\alpha}_1u(a)-\beta_1u'(a)=\gamma_1, \quad \beta_1\neq 0, \\ B_2u=\alpha_2u(b)+{\beta}_2u'(b)=\gamma_2, \quad \beta_2\neq 0. \end{cases}\end{split}\]

Ef \(\beta_1\neq 0\) og \(\beta_2\neq 0\), tökum við \(\psi_0\) sem núllfallið, þá er nálgunarfallið gefið með

\[v(x)=c_1\varphi_1(x)+\cdots+c_N\varphi_N(x), ~~~~x \in [a,b].\]

Við getum notað jaðarskilyrðin til þess að einfalda tvílínulega formið (6.10), þ.e.a.s.

\[{{\langle u,\varphi\rangle}}_L + \dfrac {p(a)}{\beta_1}(\alpha_1u(a)-\gamma_1)\varphi(a) +\dfrac{p(b)}{\beta_2}(\alpha_2u(b)-\gamma_2)\varphi(b) ={{\langle f,\varphi\rangle}}.\]

Ef við berum jöfnuna að ofan saman við jöfnu (6.9), skiljum við nú hvað \(T_B\) er og restin, þ.e.a.s mengi fallanna er

\[V_B=V,\]

línulega formið \(T_B\) er gefið með

\[T_B(\varphi)=\dfrac {p(a)\gamma_1}{\beta_1}\varphi(a) +\dfrac{p(b)\gamma_2}{\beta_2}\varphi(b), \qquad \varphi \in V_B,\]

og tvílínulega formið \({{\langle \varphi,\psi\rangle}}_{L,B}\) er gefið með

\[{{\langle \varphi,\psi\rangle}}_{L,B}={{\langle \varphi,\psi\rangle}}_L +\dfrac {p(a)\alpha_1}{\beta_1}\varphi(a)\psi(a) +\dfrac{p(b)\alpha_2}{\beta_2}\varphi(b)\psi(b), \qquad \varphi,\psi\in V_B.\]

6.4.2. Í tveimur víddum

Við viljum skoða veiku framsetninguna (6.9) fyrir jaðargildisverkefni í \(\mathbb{R}^2\). Fyrst er gagnlegt að skrifa jaðargildisverkefnið sem

\[\begin{split}\begin{cases} Lu=-\nabla\cdot (p\nabla u)+qu=f, \quad &\text{á } D\\ u=\gamma,\quad &\text{á } \ \partial D_1,\\ \alpha u+\beta\dfrac{\partial u}{\partial n} =\gamma, \quad &\text{á } \ \partial D_2, \end{cases}\end{split}\]

þar sem

\[\partial_1D=\{(x,y)\in \partial D\,;\, \beta(x,y)=0\} \qquad \text{ og } \qquad \partial_2D=\{(x,y)\in \partial D\,;\, \beta(x,y)\neq 0\},\]

og \(\partial D=\partial_1D\cup \partial_2 D\) (munið 5.3). Við gerum alltaf ráð fyrir að \(p\in C^1\) og \(q, f\) séu samfelld á \(\bar D\subset\mathbb{R}^2\).

Við höldum áfram eins og áður, þ.e.a.s.

1. Fyrst veljum við fallið \(\psi_0\) þ.a. \(\psi_0(x,y) = \gamma(x,y)\) fyrir öll \((x,y)\in\partial D_1\).

2. Eftir það, veljum við föllin \(\varphi\) þ.a. \(\varphi(x,y)=0\) fyrir \((x,y)\in\partial D_1\). Það þýðir að við veljum

\[V_B=\{ \varphi\in \mathcal{C}^2(\mathbb R)~~: ~~ \varphi(x,y)=0, ~~ (x,y)\in \partial D_1 \}.\]

3. Að lokum skilgreinum við nálgunarfallið með \(v=\psi_0+c_1\varphi_1+\cdots+c_N\varphi_N\) og við krefjumst þess að \(v\) uppfylli veiku framsetninguna (6.9).

Við sjáum nú hvað framsetningin (6.9) gefur okkur í \(\mathbb{R}^2\). Munið að í kafla 6.1.2 reiknuðum við að

\[\langle L u, \varphi\rangle= \langle u, \varphi\rangle_L - \int_{\partial D} p \dfrac{\partial u}{\partial n} \varphi ds\,,\]

en nú tökum við \(\varphi \in V_B\) og jaðarinn er \(\partial D=\partial_1D\cup \partial_2 D\), þá getum við skrifað

\[\langle L u, \varphi\rangle= \langle u, \varphi\rangle_L - \int_{\partial D_2} p \dfrac{\partial u}{\partial n} \varphi ds\ = \langle u, \varphi\rangle_L - \int_{\partial D_2} p \dfrac{\gamma -\alpha u}{\beta} \varphi ds\,,\]

þar sem í síðasta skrefi höfum við notað jaðarskilyrði í \(\partial D_2\). Nú erum við búin að skrifa niður veiku framsetninguna (6.9) fyrir nálgunarfallið \(v\) í \(\mathbb{R}^2\), þá er

(6.11)\[\langle v, \varphi\rangle_L + \int_{\partial D_2} p \dfrac{\alpha v}{\beta} \varphi ds = \langle f, \varphi\rangle + \int_{\partial D_2} p \dfrac{\gamma}{\beta} \varphi ds, \qquad \varphi\in V_B.\]

Við berum formúluna (6.11) saman við almennu stæðuna (6.9), og við sjáum að hér höfum við

\[{\langle \varphi,\psi\rangle}_{L,B}= {{\langle \varphi,\psi\rangle}}_L+\int_{\partial_2D}\dfrac{p\alpha}\beta \varphi\psi\, ds\qquad \varphi,\psi\in V_B,\]

og

\[T_B(\varphi)=\int_{\partial_2D}\dfrac{p\gamma}\beta \varphi\, ds, \qquad \varphi,\psi\in V_B.\]

6.4.3. Sýnidæmi

Dæmi

Lítum á eftirfarandi jaðargildisverkefni

(6.12)\[\begin{split}\begin{cases} -\nabla^2 u= -\dfrac{\partial^2 u}{\partial x^2 }-\dfrac{\partial^2 u}{\partial y^2 }=1 &\text{á } \ D,\\ u(x,0)=1-x, &0<x<1,\\ \dfrac{\partial u}{\partial n}(0,y)=1-y, &0<y<1,\\ \dfrac{\partial u}{\partial n}(x,1-x)+u(x,1-x)=0, &0<x<1, \end{cases}\end{split}\]

þar sem \(D\) er

\[D=\{(x,y)\, ;\, 0<x<1, 0<y<1-x\}.\]

Hér höfum við að

\[\begin{split}&&\partial D_1 =\{(x,0)\, ;\, 0\leq x\leq 1\},\\ &&\partial D_2 =\{(0,y)\, ;\, 0<y\leq 1\}\cup \{(x,1-x)\, ;\, 0< x<1\}.\end{split}\]

Við viljum nota aðferð Galerkins til þess að ákvarða nálgunarlausn af gerðinni

\[v(x,y)=a+bx+cy+dxy.\]

Við byrjum á að skoða Dirichlet skilyrði í \(\partial D_1\), og við veljum fallið \(\psi_0\) þ.a. \(\psi_0(x,0)=1-x\), fyrir \(x\in [0,1]\). Þá getum við valið

\[\psi_0(x,y)=1-x, \qquad (x,y)\in \bar D.\]

Nú veljum við \(\varphi\) þ.a. \(\varphi(x,0)=0\), fyrir \(x\in [0,1]\), þ.e.a.s.

\[V_B=\{ \varphi\in C^2(\bar D)~~: ~~\varphi(x,y)=0 \quad (x,y)\in \partial D_1 \}.\]

Við þurfum að velja \(\varphi\), en með þetta val á fallinu \(\psi_0\), er það jafngilt að setja \(a=1\) og \(b=-1\). Það vantar bara að velja föll \(\varphi_1, \varphi_2\), sem þurfa að vera núll á jaðrinum \(\partial D_1\). Við sjáum að einliður \(y\) og \(x y\) eru núll á jaðrinum \(\partial D_1\), þá getum við tekið

\[\varphi_1 (x,y)=y , \qquad \varphi_2(x,y)= x y.\]

Við beitum (6.11), en fyrst skoðum við jaðarliði í (6.11). Athugum að \(p(x,y)=1\), \(\alpha(0,y)=0\) fyrir \(y\in ]0,1]\), og \(\gamma(x,1-x)=0\) fyrir \(x\in ]0,1[\), þá er

\[\begin{split}&& \int_{\partial D_2} p \dfrac{\alpha v}{\beta} \varphi ds= \sqrt 2 \int_0^1 v(x,1-x) \varphi(x,1-x)dx, \\ && \int_{\partial D_2} p \dfrac{\gamma}{\beta} \varphi ds= \int_0^1 (1-y)\varphi(0,y)dy.\end{split}\]

Athugum að

\[\nabla \psi_0(x,y)=(-1,0)^T, \quad \nabla \varphi_1(x,y)= (0,1)^T , \quad \nabla \varphi_2(x,y)=(y,x)^T.\]

Fyrir \(\varphi_1\) verður veika framsetningin (6.11)

\[\begin{split}&&\int_D \nabla v \cdot \nabla \varphi_1 dA + \sqrt 2 \int_0^1 v(x,1-x) \varphi_1(x,1-x)dx= \int_D \varphi_1 dA+ \int_0^1 (1-y)\varphi_1(0,y)dy, \\ && c_1 \int_D dA+ c_2 \int_D x dA +\sqrt 2 \int_0^1 \left(1+c_1+c_2 x\right)(1-x)^2dx =\int_D y dA + \int_0^1 (1-y)y dy,\end{split}\]

sem gefur okkur

\[c_1(\tfrac 12 +\tfrac{\sqrt 2}{3})+c_2(\tfrac 16 +\tfrac{\sqrt 2}{12})=(\tfrac 13 +\tfrac{\sqrt 2}{3}).\]

Við höldum áfram á svipaðan hátt fyrir \(j=2\), þá er

\[\begin{split}&&\int_D \nabla v \cdot \nabla \varphi_2 dA + \sqrt 2 \int_0^1 v(x,1-x) \varphi_2(x,1-x)dx= \int_D \varphi_2 dA+ \int_0^1 (1-y)\varphi_2(0,y)dy, \\ && \int_D (-y)dA+c_1 \int_D x dA+ c_2 \int_D (x^2+y^2) dA +\sqrt 2 \int_0^1 \left(1+c_1+c_2 x\right)x(1-x)^2dx =\int_D x\, y dA,\end{split}\]

sem gefur okkur

\[c_1(\tfrac 16 +\tfrac{\sqrt 2}{12})+c_2(\tfrac 16 +\tfrac{\sqrt 2}{30})=(\tfrac{5}{24} -\tfrac{\sqrt 2}{12}).\]

Að lokum fáum við

\[c_1=-0.4360, ~~~~c_2=1.0034,\]

þá er nálgunarfallið gefið með

\[v(x,y)=1-x-0.4360\, y+1.0034\, xy.\]

6.5. Bútaaðferð í tveimur víddum

Við ætlum að líta á jaðargildisverkefni (6.3), og hér við viljum nota aðferð Galerkins þar sem svæðinu \(\bar D\) er skipt í sammengi lokaðra þríhyrninga og nálgunarfallið er línuleg samantekt af þúfugrunnföllum.

6.5.1. Net með þríhyrningum

Við skiptum svæðinu \(\bar D\) í þríhyrninga, eins og í myndunum að neðan.

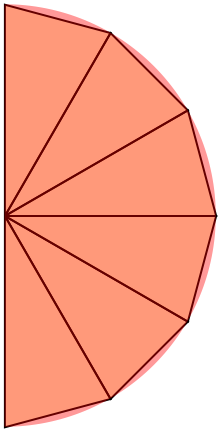
Mynd 6.1 Hálfri skífu skipt í þríhyrninga.

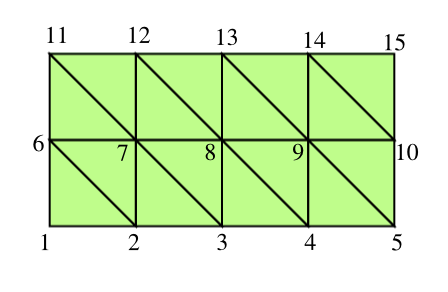
Mynd 6.2 Rétthyrningi skipt í þríhyrninga. Hér er \(N=4\) og \(M=2\).

Við skoðum dæmi með rétthyrningnum \(D\)

\[D=\{ (x,y)\in \mathbb{R}^2, ~~ a<x<b, ~~ c<y<d\}\,.\]

Þar höfum við skiptingu á \(x\)-ás

\[a=x_1 < x_2 < \dots < x_N= b, \qquad x_j= a+ (j-1)h \,,~~ j=1, \dots, N+1\,,\]

þar sem \(h=(b-a)/N\), og skiptingu á \(y\)-ás

\[c=y_1 < y_2 < \dots < y_M= d, \qquad y_p= c+ (p-1)k \,,~~ p=1, \dots, M+1\,,\]

þar sem \(k=(d-c)/M\). Hornpunktar \((x_j, y_p)\) þríhyrninganna eru allir í \(\bar D\). Við veljum að raða punktunum eins og í myndinni, þ.e.a.s. við notum vörpun

\[\sigma: (j, p) \to \alpha= \sigma(j,p)= j+(p-1)(N+1)\,, ~~ j=1, \dots, N+1\,,~~p=1, \dots, M+1\,,\]

svo er \(\alpha=1, \dots, (M+1)(N+1)\).

Sérhverjum þríhyrningi er lýst sem mengi

\[T_{A,B,C}=\{(x,y)=(1-s-t)(x_A,y_A)+s(x_B,y_B)+t(x_{C},y_{C}) \,;\, s,t\in [0,1], s+t\leq 1\},\]

þar sem \((x_A,y_A), (x_B,y_B)\) og \((x_C,y_C)\) eru hornpunktar þríhyrningsins. Á myndinni sjáum við t.d. þríhyrninginn með hornpunkta 1, 2, 6, við táknum hann með \(T_{1,2,6}\).

Athugasemd

Röð punktanna skiptir máli hér! Við röðum punktunum rangsælis eftir jaðri þríhyrningsins.

Athugum líka að

\[T_{1,2,6}=T_{6,1,2}=T_{2,6,1}.\]

Það er gagnlegt að skoða einingarþríhyrning með hornpunkta \((0,0), (1,0)\) og \((0,1)\). Við táknum hann með \(E\) og þá er

\[E=\{(s,t)\,;\, s,t\in [0,1], s+t\leq 1\}.\]

Þá getum við notað vörpun \(t_{A,B,C}\) til þess að varpa einingarþríhyrningnum í þríhyrninginn \(T_{A,B,C}\), þá er

\[\begin{split}t_{A,B,C}: ~&E \to T_{A,B,C}\\ & (s,t) \mapsto (x,y)=(1-s-t)(x_A,y_A)+s(x_B,y_B)+t(x_{C},y_{C}).\end{split}\]

Við getum umritað vörpunina á fylkjaform á eftirfarandi hátt

(6.13)\[\begin{split}\left[\begin{matrix} x \\ y \end{matrix}\right] = \left[\begin{matrix} x_A \\ y_A \end{matrix}\right]+ \left[\begin{matrix} x_B-x_A & x_C-x_A \\ y_B-y_A & y_C-y_A \end{matrix}\right] \left[\begin{matrix} s\\ t \end{matrix}\right].\end{split}\]

Athugum að vörpunin er gagntæk, og andhverfan \(t^{-1}_{A,B,C}\) er gefin með

\[\begin{split}t^{-1}_{A,B,C}: ~&T_{A,B,C} \to E\\ & \left[\begin{matrix} x\\ y \end{matrix}\right] \mapsto \left[\begin{matrix} s\\ t \end{matrix}\right] = \frac{1}{d}\left[\begin{matrix} y_C-y_A & -(x_C-x_A) \\ -(y_B-y_A) & x_B-x_A \end{matrix}\right] \left[\begin{matrix} x-x_A\\ y-y_A \end{matrix}\right],\end{split}\]

þar sem \(d\) er ákveða fylksins í (6.13).

Seinna munum við nota flatarmál þríhyrningsins \(T_{A,B,C}\) og massamiðju \(M_{A,B,C}\), og þau eru gefin með

\[\begin{split}&& area(T_{A,B,C})= \frac{|d|}{2}, \\ && M_{A,B,C}=\tfrac 13\big((x_A,y_A)+(x_B,y_B)+(x_C,y_C)\big).\end{split}\]

6.5.2. Þúfugrunnföll

Við ætlum að nota þúfugrunnföll til þess að nálga lausn á (6.3). Við skilgreinum þúfugrunnföll á \(\bar D\) á eftirfarandi hátt:

\[\begin{split}&&\varphi_A: T_{A,B,C} \to [0,1] \,, \text{þ.a.}~~ \varphi(x_A,y_A)=1\,, ~~\varphi(x_B,y_B)=\varphi(x_C,y_C)=0 \, \\ && \varphi_A ~~\text{er samfellt og línulegt}.\end{split}\]

Við sjáum í dæmi að neðan graf fallsins \(\varphi_3\) fyrir einingarþríhyrninginn \(E_{1,2,3}\). Það er ljóst að graf fallsins \(\varphi_A\) er plan í \(\mathbb{R}^3\) sem tengir punktana

\[(x_A,y_A,1), ~~~ (x_B,y_B,0), ~~~ (x_C,y_C,0).\]

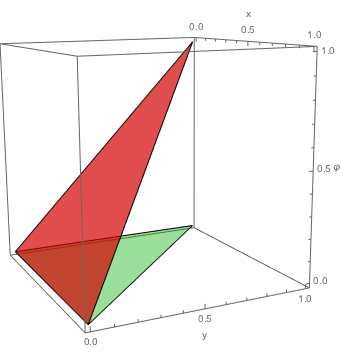
Mynd 6.3 Dæmi um graf fallsins \(\varphi_3\) skilgreint yfir einingarþríhyrninginn \(E_{1,2,3}\).

Við skilgreinum fall \(\varphi_E\) eins og grunnfallið á einingarþríhyrningnum \(E\) sem tekur gildið 1 í punktinum \((0,0)\). Þá er

\[\varphi_E(s,t)=1-s-t, \qquad (s,t)\in E,\]

og við fáum \(\varphi_E(0,0)=1\) og \(\varphi_E(1,0)=\varphi_E(0,1)=0\).

Hvernig getum við smíðað fallið \(\varphi_A\) alment? Við notum vörpunina \(t_{A,B,C}\), þ.e.a.s. við vörpum þríhyrningnum \(T_{A,B,C}\) í einingarþríhyrninginn \(E\) og við lesum úr því \(\varphi_E\), þ.e.

\[\varphi_A(x,y)=\varphi_E(t_{A,B,C}^{-1}(x,y)).\]

Ef við viljum t.d. skrifa niður \(\varphi_A\), þá er

(6.14)\[\varphi_A(x,y)=\tfrac 1d \left((x_C-x_B)y-(y_C-y_B)x+x_B y_C-x_C y_B\right),\]

og það er ljóst að \(\varphi_A(x_B,y_B)=\varphi_A(x_C,y_C)=0\) og \(\varphi_A(x_A,y_A)=1\).

Athugum að fallið \(\varphi_B\) á \(T_{A,B,C}\), sem er skilgreint eins og \(\varphi_B(x_A,y_A)=\varphi_B(x_C,y_C)=0\) og \(\varphi_B(x_B,y_B)=1\), er gefið með

(6.15)\[\varphi_B(x,y)=\tfrac 1d \left((x_A-x_C)y-(y_A-y_C)x+x_C y_A-x_A y_C\right).\]

Það er hjálplegt að skoða einginleika fallanna \(\varphi_A\), af því að við ætlum að nota þá til þess að reikna út veiku framsetningu jaðargildisverkefnisins.

Eiginleikar þúfugrunnfallanna

Fyrst ætlum við að skoða eiginleika þúfugrunnfallanna sem við munum nota seinna. Við lítum á \(\varphi_A\) og \(\varphi_B\) sem eru skilgreind á (6.14) og (6.15).

1. Stigull fallsins \(\varphi_A\) er gefinn með

\[\nabla\varphi_A(x,y)={1\over d}\left(-(y_C-y_B),(x_C-x_B)\right).\]

2. Þá er eftirfarandi heildi gefið með

\[\int_{T_{A,B,C}}\nabla\varphi_A \cdot \nabla\varphi_A \,dx dy={1\over 2 |d|} \left((x_C-x_B)^2+(y_C-y_B)^2\right).\]

3. Fyrir eftirfarandi heildi, fáum við

\[\int_{T_{A,B,C}}\nabla\varphi_A \cdot \nabla\varphi_B\, dx dy={1\over 2 |d|} \left(-(x_B-x_C)(x_A-x_C)-(y_B-y_C)(y_A-y_C)\right).\]

4. Athugum að

\[\varphi_A(M_{C,B,C})=\varphi_A\left(\tfrac 13(x_A+x_B+x_C),\tfrac 13(y_A+y_B+y_C)\right)=\tfrac 13.\]

Ritháttur í kennslubókinni

Við getum notað sama rithátt og í kennslubókinni, þá skilgreinum við eftirfarandi hliðarvigra

\[{\mathbf l}_A=(x_C-x_B,y_C-y_B), \qquad {\mathbf l}_B=(x_A-x_C,y_A-y_C), \qquad {\mathbf l}_C=(x_B-x_A,y_B-y_A).\]

Við sjáum að hliðarvigrarnir liggja á mótlægum hliðum \(T_{A,B,C}\) við hornpunkta númer \(A, B\) og \(C\) miðað við rangsælis umferðarstefnu eftir jaðrinum.

Við snúum hliðarvigrunum um \(\pi/2\) réttsælis og þá fáum við

\[{\mathbf l}_A^R=(y_C-y_B,-x_C+x_B,), \qquad {\mathbf l}_B^R=(y_A-y_C,-x_A+x_C,), \qquad {\mathbf l}_C^R=(y_B-y_A,-x_B+x_A,).\]

Vigrarnir \({\mathbf l}_A^R, {\mathbf l}_B^R, {\mathbf l}_C^R\) eru hornréttir á hliðarnar á móti hornum númer \(A, B\) og \(C\) og snúa í stefnu ytri þvervigurs. Sjáið mynd fyrir einingarþríhyrninginn \(E\).

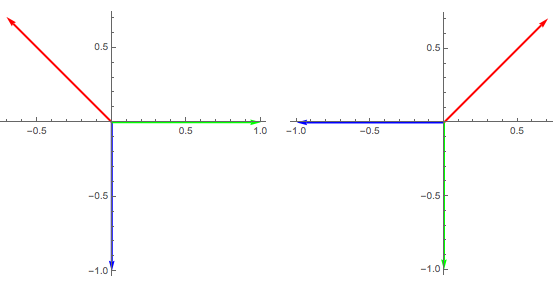
Mynd 6.4 Hliðarvigrarnir \({\mathbf l}_A, {\mathbf l}_B, {\mathbf l}_C\) (rautt, blátt og grænt) til vinstri og vigrarnir \({\mathbf l}_A^R, {\mathbf l}_B^R, {\mathbf l}_C^R\) til hægri (rautt, blátt og grænt).

Þá getum við notað hliðarvigrana til þess að skrifa niður eiginleika þúfugrunnfallanna, þ.e.

1. Stigull fallsins \(\varphi_A\) er gefinn með

\[\nabla\varphi_A(x,y)=-{{\mathbf l}_A^R\over d},\]

og líka fyrir föllin \(\varphi_B, \varphi_C\),

\[\nabla\varphi_B(x,y)=-{{\mathbf l}_B^R\over d},\qquad \nabla\varphi_C(x,y)=-{{\mathbf l}_C^R\over d}.\]

2. Innfeldi stiglanna er gefið með

\[\nabla\varphi_\alpha(x,y)\cdot \nabla\varphi_\beta(x,y)={{\mathbf l}_\alpha^R\cdot {\mathbf l}_\beta^R\over d^2}={{\mathbf l}_\alpha\cdot {\mathbf l}_\beta\over d^2}, \qquad \alpha, \beta=A, B, C.\]

6.5.3. Dirichlet-verkefni

Mynd 6.5 Rétthyrningi skipt í þríhyrninga. Hér er \(N=4\) og \(M=2\).

Munið að við viljum finna lausn á eftirfarandi jaðargildisverkefni

\[\begin{split}\begin{cases} Lu=-\nabla\cdot (p\nabla u)+qu=f, \quad &\text{á } D\\ u={\gamma},\quad &\text{á } \ \partial D\,, \end{cases}\end{split}\]

þar sem \(D\) er gefið með

\[D=\{ (x,y)\in \mathbb{R}^2, ~~ a<x<b, ~~ c<y<d\}\,.\]

Við gerum alltaf ráð fyrir að \(p\in C^1\) og \(q, f\) séu samfelld á \(\bar D\subset\mathbb{R}^2\).

Við skiptum \(D\) í þríhyrninga eins og í mynd að ofan og eins og við gerðum í 6.5.1.

Við táknum með

1. \(S\) sammengi þríhyrninganna á svæðinu \(\bar D\),

2. \(Q\) mengi talna sem svara til punktanna á \(\partial D\) sem uppfylla Dirichlet jaðarskilyrði,

3. \(R\) mengi talna sem svara til punktanna á \(D\),

4. \(P\) fjölda allra punkta, athugum að \(P=(N+1)(M+1)\),

Við skilgreinum nálgunarfallið sem

\[v(x,y)=\sum_{\alpha=1}^P c_\alpha\varphi_\alpha(x,y), \qquad (x,y)\in S.\]

Athugum að \(\alpha=1,\dots, P\) og við notun vörpunina \(\alpha=\sigma(j,p)=j+(p-1) (N+1)\).

1. Innri punktar

Fyrir innri punkta þurfum við að finna nálgunarformúlur, og við notum veiku framsetninguna. Munið að veika framsetningin er þá

\[\langle \mathcal L u, \varphi_\beta\rangle= \langle u, \varphi_\beta \rangle_L=\langle f, \varphi_\beta\rangle,\qquad \beta\in R.\]

Nú erum við búin og getum reiknað út veiku framsetninguna fyrir nálgunarfallið og \(\varphi_\beta\) með \(\beta\in R\).

Á vinstri hliðinni höfum við

\[\langle v, \varphi_\beta \rangle_L = \sum_{\alpha=1}^P c_\alpha \int_S \left(p \nabla \varphi_\alpha \cdot \nabla \varphi_\beta +q \varphi_\alpha \varphi_\beta\right) dA.\]

Á hægri hliðinni höfum við

\[\langle f, \varphi_\beta\rangle= \int_S f\varphi_\beta dA.\]

Á fylkjaformi \(A{\mathbf c}={\mathbf b}\) er

\[\begin{split}&& a_{\beta, \alpha}= \int_S \left(p \nabla \varphi_\alpha \cdot \nabla \varphi_\beta +q \varphi_\alpha \varphi_\beta\right) dA\,, \\ && b_\beta = \int_S f\varphi_\beta dA\,.\end{split}\]

Nú þurfum við að reikna út heildin að ofan. Við nálgum þau með því að nota reglu „miðpunktanna“, það þýðir að fyrir sérhvert samfellt fall \(\psi\) nálgum við heildi yfir þríyrning \(T_{A,B,C}\) á eftirfarandi hátt

\[\int_{T_{A,B,C}} \psi(x,y)dA\approx \psi\left(\tfrac{x_A+x_B+x_C}{3},\tfrac{y_A+y_B+y_C}{3}\right) area(T_{A,B,C}) ={|d|\over 2}\psi(M_{A,B,C})\,\]

þar sem \(M_{A,B,C}\) er massmiðja þríhyrningsins \(T_{A,B,C}\).

Við skoðum ýmsa liði.

1. Í \(b_\beta\) höfum við

\[\int_S f\varphi_\beta dA\approx \sum_{T_{\beta}}f(M_{(\beta)}){|d|\over 6},\]

af því að \(\varphi_\beta(M_{(\beta)})=\tfrac 13\). Athugum að summan hér þýðir að við þurfum að summa bara yfir þríhyrninga sem hafa punkt \(\beta\) fyrir hornpunkt (munið skilgreinguna á þúfugrunnföllum).

2. Í \(b_\beta\) og í \(a_{\beta \alpha}\) höfum við

\[\int_S p \nabla \varphi_\alpha \cdot \nabla \varphi_\beta dA \approx \sum_{T_{\beta}} p(M_{(\beta)}){{\mathbf l}_\alpha^R\cdot {\mathbf l}_\beta^R\over 2|d|}=\sum_{T_{\beta}} p(M_{(\beta)}){{\mathbf l}_\alpha\cdot {\mathbf l}_\beta\over 2|d|},\]

þar sem summan er yfir þríhyrninga sem hafa punkt \(\beta\) fyrir hornpunkt. Munið að innfeldi \(\nabla \varphi_\alpha \cdot \nabla \varphi_\beta\) er ekki núll aðeins ef \(\alpha\) og \(\beta\) eru tveir hornpunktar \(T_{\beta}\).

3. Í \(b_\beta\) og í \(a_{\beta \alpha}\) höfum við

\[\int_S q \varphi_\alpha \varphi_\beta dA \approx \sum_{T_{\beta}} q(M_{(\beta)}){|d|\over 18},\]

af því að \(\varphi_\beta(M_{(\beta)})=\tfrac 13\). Aftur, við summun yfir þríhyrninga sem hafa punkt \(\beta\) fyrir hornpunkt.

Athugið

Í kennslubókinni er heildið að ofan nálgað á eftirfarandi hátt

\[\int_{T_{A,B,C}} \psi(x,y)\, dA \approx \tfrac{|d|}{6}\big(\psi_{A,B}+\psi_{B,C}+\psi_{C,A}\big),\]

þar sem \(\psi\) er samfellt fall, \(\psi_{A,B}, \psi_{B,C}\) og \(\psi_{C,A}\) tákna gildi fallsins \(\psi\) í miðpunktum hliðanna \(AB, BC\) og \(CA\).

Af 2. og 3. leiðir að

\[\int_S \left(p \nabla \varphi_\alpha \cdot \nabla \varphi_\beta + q \varphi_\alpha \varphi_\beta\right) dA \approx \sum_{T_{\beta}}\left(p(M_{(\beta)}){{\mathbf l}_\alpha\cdot {\mathbf l}_\beta\over 2|d|}+q(M_{(\beta)}){|d|\over 18}\right).\]

Athugið

Í kennslubókinni er heildið að ofan nálgað á eftirfarandi hátt

\[\begin{split}\int_{S}\big(p\nabla \varphi_\alpha\cdot \nabla \varphi_\beta +q\varphi_\alpha\varphi_\beta\big)\, dA \approx \sum_{T_{\beta}}\dfrac {p(M_{(\beta)})}{2 |d|}{{\mathbf l}_\alpha\cdot {\mathbf l}_\beta} +\sum_{T_{\beta}}\begin{cases} \tfrac 1{12} q(M_{(\beta)})\, |d|,& \alpha=\beta,\\ \tfrac 1{24} q(M_{(\beta)})\, |d|,& \alpha\neq \beta. \end{cases}\end{split}\]

Að lokum, fáum við fyrir innri punktana

\[\begin{split}&& a_{\beta \alpha}=\sum_{T_{\beta}}\left(p(M_{(\beta)}){{\mathbf l}_\alpha\cdot {\mathbf l}_\beta\over 2|d|}+q(M_{(\beta)}){|d|\over 18}\right)\\ && b_\beta=\sum_{T_{\beta}}f(M_{(\beta)}){|d|\over 6}\end{split}\]

þar sem \(\beta\in R\), summan \(\sum_{T_{\beta}}\) þýðir að við þurfum að summa bara yfir þríhyrninga sem hafa punkt \(\beta\) fyrir hornpunkt, og innfeldi \({{\mathbf l}_\alpha}\cdot {\mathbf l}_\beta\) er núll ef \(\alpha\) og \(\beta\) eru ekki tveir hornpunktar \(T_{\beta}\).

2. Punktar á jaðrinum

Við þurfum að krefjast að \(v\) uppfyllir Dirichlet-jaðarskylirði, þess vegna setjum við

\[\begin{split}&& a_{\beta \beta}=1\,,\\ && a_{\alpha \beta}=0\,, \quad \text{ef} \quad \alpha\neq \beta \\ && b_\beta=\gamma(x_j, y_p)\,,\end{split}\]

fyrir \(\beta\in Q\).

6.5.4. Sýnidæmi

Dæmi

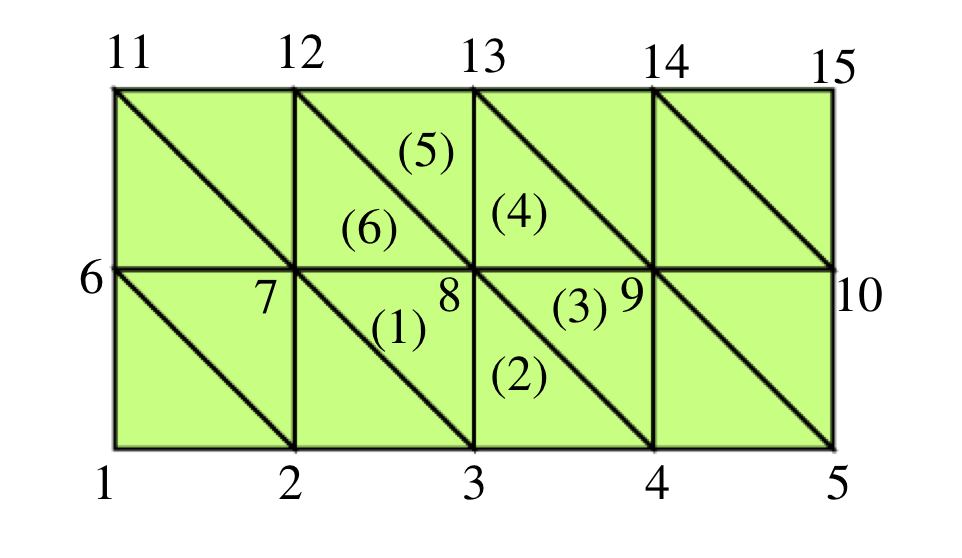
Mynd 6.6 Rétthyrningi skipt í þríhyrninga. Hér er \(N=4\) og \(M=2\).

Við lítum á Dirichlet jaðarskilyrði, þ.e.

\[\begin{split}\begin{cases} -\nabla^2 u +q u= f \qquad D\\ u=\gamma \qquad \partial D, \end{cases}\end{split}\]

þar sem svæði \(D\) er \(D=\{(x,y)\in \mathbb{R}^2~~: x\in]a, b[, ~~ y\in ]c, d[\}\). Við notum net eins og á myndinni að ofan, eins og við gerðum í 6.5.1.

Hornpunktar \(1,2,3,4,5,6,10,11,12,13,14\) og 15 eru í \(\partial D_1\). Innri punktar eru 7,8 og 9.

Skoðum \(\beta=8\). Það eru 6 þríhyrningar sem hafa \(\beta=8\) fyrir hornpunkt. Það þýðir að þegar við reiknum \(a_{\beta=8,\alpha}\), eru einu stök fylkisins sem eru ekki núll þau sem hafa \(\alpha=7,3,4,9,13,12\).

Þegar við skiptum bilinu í jafna hluta, eins og við gerðum í 6.5.1, þá er

\[area(T)={|d|\over 2} ={h k\over 2},\]

og

\[\int_S \nabla \phi_\beta\cdot \nabla \phi_\beta dA= {1\over 2 h k}\left(2 h^2+2 k^2 +2 (k^2+h^2)\right)= {2\over h k}\left(k^2+h^2\right),\]

\[\int_S q \phi_\beta \phi_\beta dA= {h k\over 18} \left(q(M_1)+q(M_2)+q(M_3)+q(M_4)+q(M_5)+q(M_6)\right),\]

þar sem \(M_i\) eru miðjupunktar fyrir 6 þríhyrninga sem hafa \(\beta\) fyrir hornpunkt.

Þetta gefur fyrir \(\beta=8\)

\[a_{\beta,\beta}=\tfrac{2}{h k}(k^2+h^2) +{h k\over 18} \left(q(M_1)+q(M_2)+q(M_3)+q(M_4)+q(M_5)+q(M_6)\right).\]

Fyrir \(\alpha\neq \beta=8\), fáum við

\[\int_S \nabla \phi_\alpha\cdot \nabla \phi_\beta dA=0 \quad \alpha=4, 12\]

af því að hliðarvigrarnir \(\mathbf{l}_\alpha,\mathbf{l}_\beta\) eru hornréttir. Ennfremur höfum við

\[\int_S q \phi_\alpha \phi_\beta dA={hk\over 18}(q(M_{2(5)})+q(M_{3(6)})) \quad \alpha=4, 12,\]

og það gefur

\[a_{\beta,\alpha}={hk\over 18}(q(M_{2(5)})+q(M_{3(6)})) \qquad \text{með}\qquad \alpha=\sigma(j+1,p-1), \alpha=\sigma(j-1,p+1).\]

Athugum að við notum \(\beta=\sigma(j,p)\).

\[\int_S \nabla \phi_\alpha\cdot \nabla \phi_\beta dA=-{h^2\over 2 h k} 2=-{h\over k} \quad \alpha=3, 13,\]

af því að hliðarvigurinn \(\mathbf{l}_\alpha\) er láréttur, og það eru tveir þríhyrningar sem hafa \(\alpha, \beta\) fyrir hornpunkta.

Ennfremur höfum við

\[\int_S q \phi_\alpha \phi_\beta dA={hk\over 18}(q(M_{1(4)})+q(M_{2(5)})) \quad \alpha=3, 13,\]

og það gefur

\[a_{\beta,\alpha}=-{h\over k}+{hk\over 18}(q(M_{1(4)})+q(M_{2(5)})) \qquad \text{með}\qquad \alpha=\sigma(j,p-1),\alpha=\sigma(j,p+1) .\]

\[\int_S \nabla \phi_\alpha\cdot \nabla \phi_\beta dA=-{k^2\over 2 h k} 2=-{k\over h} \quad \alpha=7, 9,\]

af því að hliðarvigurinn \(\mathbf{l}_\alpha\) er lóðréttur, og það eru tveir þríhyrningar sem hafa \(\alpha, \beta\) fyrir hornpunkta.

Ennfremur höfum við

\[\int_S q \phi_\alpha \phi_\beta dA={hk\over 18}(q(M_{6(4)})+q(M_{1(3)})) \quad \alpha=7, 9,\]

og það gefur

\[a_{\beta,\alpha}=-{k\over h} +{hk\over 18}(q(M_{6(4)})+q(M_{1(3)})) \qquad \text{með}\qquad \alpha=\sigma(j-1,p),\alpha=\sigma(j+1,p).\]

Skoðum vigurinn \(\mathbf b\), þá er

\[b_\beta=\langle f, \varphi_\beta\rangle= \frac{h k}{6} \left(f(M_1)+f(M_2)+f(M_3)+f(M_4)+f(M_5)+f(M_6)\right).\]

Við þurfum að endurtaka aðferðina fyrir \(\beta=7,8,9\).

Fyrir jaðarpunkta þurfum við að setja

\[a_{\beta,\beta }=1, \qquad b_\beta=\gamma(x_j, y_p),\]

þar sem \(\beta=\sigma(j,p)\).

6.5.5. Jaðargildisverkefni með Neumann jaðarskilyrðum

Mynd 6.7 Rétthyrningi skipt í þríhyrninga. Hér er \(N=4\) og \(M=2\).

Við viljum finna lausn á eftirfarandi jaðargildisverkefni

\[\begin{split}\begin{cases} Lu=-\nabla\cdot (p\nabla u)+qu=f, \quad &\text{á } D\\ u={\gamma},\quad &\text{á } \ \partial D_1,\\ \dfrac{\partial u}{\partial n} =0, \quad &\text{á } \ \partial D_2, \end{cases}\end{split}\]

þar sem

\[\partial_1D=\{(x,y)\in \partial D\,;\, \beta(x,y)=0\} \qquad \text{ og } \qquad \partial_2D=\{(x,y)\in \partial D\,;\, \beta(x,y)\neq 0\},\]

og \(\partial D=\partial_1D\cup \partial_2 D\) (munið 5.3). Við gerum alltaf ráð fyrir að \(p\in C^1\) og \(q, f\) séu samfelld á \(\bar D\subset\mathbb{R}^2\).

Ennfremur, \(D\) er \(D=\{(x,y)\in \mathbb{R}^2~~: a < x <b, ~~ c< y < d\}\). Við notum net eins og á myndinni að ofan, eins og við gerðum í 6.5.1.

Við táknum með

1. \(S\) sammengi þríhyrninganna á svæðinu \(\bar D\),

2. \(Q\) mengi talna sem svara til punktanna á \(\partial D_1\) sem uppfylla Dirichlet jaðarskilyrði,

3. \(R\) mengi talna sem svara til punktanna á \(\partial D_2 \cup D\),

4. \(P\) fjölda allra punkta, athugum að \(P=(N+1)(M+1)\),

Við skilgreinum nálgunarfallið sem

\[v(x,y)=\sum_{\alpha=1}^P c_\alpha\varphi_\alpha(x,y), \qquad (x,y)\in S.\]

Munið að \(\alpha=\sigma(j,p)=j+(N+1)(p-1)\).

Við þurfum að finna nálgunarformúlur, eins og áður viljum við nota veiku framsetninguna. Athugum að við ætlum að nota veiku framsetninguna eins og í 6.5.3.

Þá gildir fyrir \(\varphi_\beta\) með \(\beta\in R\)

\[\langle \mathcal L u, \varphi_\beta\rangle= \langle u, \varphi_\beta \rangle_L =\langle f, \varphi_\beta\rangle, \qquad \beta\in R.\]

Nú erum við búin og getum reiknað út veiku framsetninguna fyrir nálgunarfallið og \(\varphi_\beta\) með \(\beta\in R\). Við nálgun heildi eins og í 6.5.3.

Skoðum

1. Innri punkta og punkta á \(\partial D_2\)

Við getum notað niðurstöður úr kafla 6.5.3. Þá er

\[\begin{split}&& a_{\beta \alpha}=\sum_{T_{\beta}}\left(p(M_{(\beta)}){{\mathbf l}_\alpha\cdot {\mathbf l}_\beta\over 2|d|}+q(M_{(\beta)}){|d|\over 18}\right)\\ && b_\beta=\sum_{T_{\beta}}f(M_{(\beta)}){|d|\over 6}\end{split}\]

þar sem \(\beta\in R\), summan \(\sum_{T_{\beta}}\) þýðir að við þurfum að summa bara yfir þríhyrninga sem hafa punkt \(\beta\) fyrir hornpunkt, og innfeldi \({{\mathbf l}_\alpha}\cdot {\mathbf l}_\beta\) er núll ef \(\alpha\) og \(\beta\) eru ekki tveir hornpunktar \(T_{\beta}\).

Athugið að mismunurinn á innri punktunum og punktunum á \(\partial D_2\) er í fjölda þríhyrninga sem hafa punkt \(\beta\) fyrir hornpunkt. Ef \(\beta\) er á \(\partial D_2\), þá höfum við aðeins þrjá þríhyrninga sem hafa punkt \(\beta\) fyrir hornpunkt (en ekki sex þríhyrninga eins og fyrir innri punkta).

2. Punktar á \(\partial D_1\)

Eins og áður höfum við

\[\begin{split}&& a_{\beta \beta}=1\,,\\ && a_{\alpha \beta}=0\,, \quad \text{ef} \quad \alpha\neq \beta \\ && b_\beta=\gamma(x_j, y_p)\,,\end{split}\]

fyrir \(\beta\in Q\).

6.5.6. Sýnidæmi

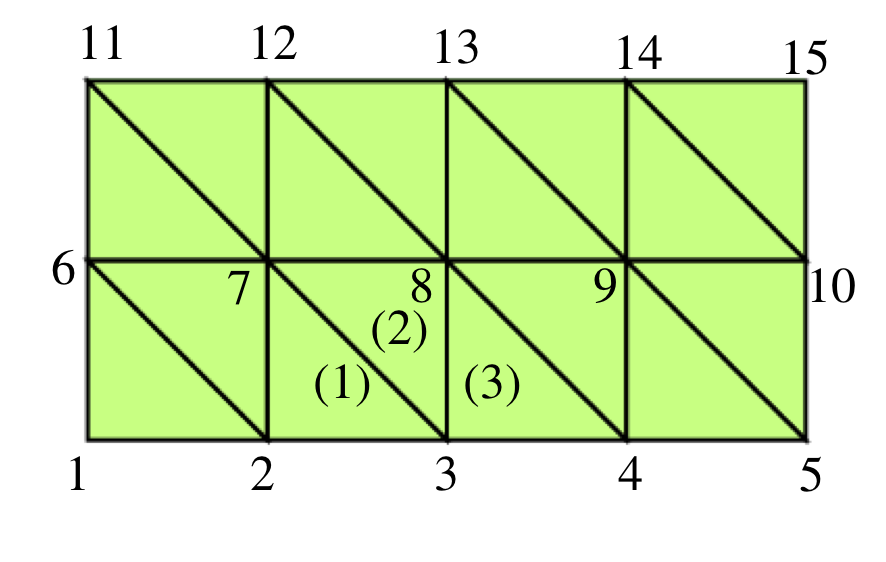
Mynd 6.8 Rétthyrningi skipt í þríhyrninga. Hér er \(N=4\) og \(M=2\).

Lítum á eftirfarandi jaðagildisverkefni

\[\begin{split}\begin{cases} Lu=-\nabla\cdot\nabla u+qu=f, \quad &\text{á } D\\ u={\gamma},\quad &\text{á } \ \partial D_1,\\ \dfrac{\partial u}{\partial n} =0, \quad &\text{á } \ \partial D_2, \end{cases}\end{split}\]

þar sem

\[\begin{split}&& D=\{ (x,y)\in \mathbb{R}^2, ~~ a<x<b, ~~ c<y<d\}\,, \\ &&\partial D_1 =\{ (x,y)\in \mathbb{R}^2, ~~ (a,y),~~ c\le y\le d\}\cup \{ (x,y)\in \mathbb{R}^2, ~~ (b,y),~~ c\le y\le d\}\,, \\ &&\partial D_2 =\partial D\setminus\partial D_1\,.\end{split}\]

og \(q, f\) séu samfelld á \(\bar D\subset\mathbb{R}^2\). Við skiptum \(D\) í þríhyrninga eins og í mynd að ofan og eins og við gerðum í 6.5.1.

Hornpunktar \(1,6,11\) og \(5,10,15\) eru í \(\partial D_1\). Innri punktar eru \(7,8\) og \(9\). Hornpunktar \(2,3,4\) og \(12,13,14\) eru í \(\partial D_2\).

1. Innri punktar.

Fyrir innri punkta fáum við niðurstödur eins og í sýnidæmi.

2. Punktar á \(\partial D_2\).

Skoðum \(\beta=3\) (sjáið mynd að ofan). Það eru 3 þríhyrningar sem hafa \(\beta=3\) fyrir hornpunkt. Það þýðir að þegar við reiknum \(a_{\beta=3,\alpha}\), eru einu stök fylkisins sem eru ekki núll þau sem hafa \(\alpha=2,3,4,7,8\).

2a. Ef \(\alpha=3\):

\[\begin{split}&&a_{\beta,\beta}=\tfrac{1}{2 h k}(k^2+h^2 +k^2+h^2) +{h k\over 18} \left(q(M_1)+q(M_2)+q(M_3)\right)\\ &&= \tfrac{k^2+h^2}{ h k}+{h k\over 18} \left(q(M_1)+q(M_2)+q(M_3)\right).\end{split}\]

Fyrir \(\alpha\neq \beta=3\), fáum við

2b. Ef \(\alpha=2, 4\):

\[\int_S \nabla \phi_\alpha\cdot \nabla \phi_\beta dA=-\tfrac{k^2}{2 hk} \quad \alpha=2, 4,\]

af því að hliðarvigurinn \(\mathbf{l}_\beta\) er lóðréttur, og það er einn þríhyrningur sem hefur \(\alpha, \beta\) fyrir hornpunkta.

\[\int_S q \phi_\alpha \phi_\beta dA={hk\over 18}q(M_{1(3)}) \quad \alpha=2, 4,\]

og það gefur

\[a_{\beta,\alpha}=-\tfrac{k}{2h}+{hk\over 18}q(M_{1(3)}) \qquad \text{með}\qquad \alpha=\sigma(j-1,p), \alpha=\sigma(j+1,p).\]

Athugum að við notum \(\beta=\sigma(j,p)\).

2c. Ef \(\alpha=8\):

\[\int_S \nabla \phi_\alpha\cdot \nabla \phi_\beta dA=-{h^2\over 2 h k} 2=-{h\over k} \quad \alpha=8,\]

Athugið að það eru tveir þríhyrningar sem hafa \(\alpha, \beta\) fyrir hornpunkta.

Ennfremur höfum við

\[\int_S q \phi_\alpha \phi_\beta dA={hk\over 18}(q(M_{2})+q(M_{3})) \quad \alpha=8,\]

og það gefur

\[a_{\beta,\alpha}=-{h\over k}+{hk\over 18}(q(M_{2)})+q(M_{3})) \qquad \text{með}\qquad \alpha=\sigma(j,p+1) .\]

2d. Ef \(\alpha=7\):

\[\int_S \nabla \phi_\alpha\cdot \nabla \phi_\beta dA=0 \qquad \text{með}\qquad \alpha=7,\]

af því að hliðarvigrarnir \(\mathbf{l}_\alpha\) og \(\mathbf{l}_\beta\) eru hornréttir.

Ennfremur höfum við

\[\int_S q \phi_\alpha \phi_\beta dA={hk\over 18}(q(M_{1})+q(M_{2})) \quad \alpha=7\]

af því að það eru tveir þríhyrningar sem hafa \(\alpha, \beta\) fyrir hornpunkta,

og það gefur

\[a_{\beta,\alpha}={hk\over 18}(q(M_{1})+q(M_{2})) \qquad \text{með}\qquad \alpha=\sigma(j-1,p+1).\]

Skoðum vigurinn \(\mathbf b\), þá er

\[b_\beta=\langle f, \varphi_\beta\rangle= \frac{h k}{6} \left(f(M_1)+f(M_2)+f(M_3)\right).\]

Við þurfum að endurtaka aðferðina fyrir \(\beta=2,3,4\).

3. Fyrir jaðarpunkta á \(\partial D_1\) þurfum við að setja

\[a_{\beta,\beta }=1, \qquad b_\beta=\gamma(x_j, y_p),\]

þar sem \(\beta=\sigma(j,p)\).

6.5.7. Jaðargildisverkefni með almennum jaðarskilyrðum eins og kennslubókinni

Mynd 6.9 Rétthyrningi skipt í þríhyrninga. Hér er \(N=4\) og \(M=2\).

Munið að við viljum finna lausn á eftirfarandi jaðargildisverkefni

\[\begin{split}\begin{cases} Lu=-\nabla\cdot (p\nabla u)+qu=f, \quad &\text{á } D\\ u={\gamma\over \alpha},\quad &\text{á } \ \partial D_1,\\ \alpha u+\beta\dfrac{\partial u}{\partial n} =\gamma, \quad &\text{á } \ \partial D_2, \end{cases}\end{split}\]

þar sem

\[\partial_1D=\{(x,y)\in \partial D\,;\, \beta(x,y)=0\} \qquad \text{ og } \qquad \partial_2D=\{(x,y)\in \partial D\,;\, \beta(x,y)\neq 0\},\]

og \(\partial D=\partial_1D\cup \partial_2 D\) (munið 5.3). Við gerum alltaf ráð fyrir að \(p\in C^1\) og \(q, f\) séu samfelld á \(\bar D\subset\mathbb{R}^2\).

Við táknum með

1. \(S\) sammengi þríhyrninganna á svæðinu \(\bar D\),

2. \(Q\) mengi talna sem svara til punktanna á \(\partial D_1\) sem uppfylla Dirichlet jaðarskilyrði,

3. \(R\) mengi talna sem svara til punktanna á \(\partial D_2 \cup D\),

4. \(P\) fjölda allra punkta, athugum að \(P=(N+1)(M+1)\),

5. \(\partial S_1\) sammengi línustrika sem tengja hornpunkta á \(\partial D_1\) (athugum að ef t.d. \(\bar D\) er rétthyrningur, þá er \(\partial S_1=\partial D_1\))

6. \(\partial S_2\) sammengi línustrika sem nálga \(\partial D_2\).

Við skilgreinum nálgunarfallið sem

\[v(x,y)=\psi_0(x,y)+\sum_{\alpha\in R} c_\alpha\varphi_\alpha(x,y), \qquad (x,y)\in S.\]

Við veljum fallið \(\psi_0\) þ.a. það hefur gildi \({\gamma\over \alpha}\) á jaðrinum \(\partial D_1\), þá er

\[\psi_0(x,y)=\sum_{\alpha\in Q} {\gamma_\alpha\over \alpha_\alpha} \varphi_\alpha(x,y),\]

þar sem við höfum táknað \(\gamma(x_i, y_j)\) með \(\gamma_\alpha\) og munið að \(\alpha=\sigma(i,j)=i+(N+1)(j-1)\) og \((x_i,y_j)\in \partial D_1\). Athugum að \({\gamma_\alpha\over \alpha_\alpha}\) er bara rauntala.

Þá gildir fyrir \(\varphi_\beta\) með \(\beta\in R\)

\[\langle \mathcal L u, \varphi_\beta\rangle= \langle u, \varphi_\beta \rangle_L -\int_{\partial S_2} p\dfrac{\partial u}{\partial n} \varphi_\beta ds= \langle u, \varphi_\beta \rangle_L +\int_{\partial S_2} p\frac{\alpha}{\beta} u\varphi_\beta ds-\int_{\partial S_2} p\frac{\gamma}{\beta} \varphi_\beta ds.\]

Veika framsetningin er þá

\[\langle u, \varphi_\beta \rangle_L +\int_{\partial S_2} p\frac{\alpha}{\beta} u\varphi_\beta ds= \langle f, \varphi_\beta\rangle+ \int_{\partial S_2} p\frac{\gamma}{\beta} \varphi_\beta ds, \qquad \beta\in R.\]

Nú erum við búin og getum reiknað út veiku framsetninguna fyrir nálgunarfallið og \(\varphi_\beta\) með \(\beta\in R\).

Á vinstri hliðinni höfum við

\[\langle v, \varphi_\beta \rangle_L = \sum_{\alpha\in R} c_\alpha \int_S \left(p \nabla \varphi_\alpha \cdot \nabla \varphi_\beta +q \varphi_\alpha \varphi_\beta\right) dA +\sum_{\alpha\in Q} {\gamma_\alpha\over \alpha_\alpha} \int_S \left(p \nabla \varphi_\alpha \cdot \nabla \varphi_\beta +q \varphi_\alpha \varphi_\beta\right) dA,\]

\[\int_{\partial S_2} p\frac{\alpha}{\beta} v\varphi_\beta ds= \sum_{\alpha\in R} c_\alpha\int_{\partial S_2} p\frac{\alpha}{\beta} \varphi_\alpha \varphi_\beta ds+ \sum_{\alpha\in Q} {\gamma_\alpha\over \alpha_\alpha} \int_{\partial S_2}p\frac{\alpha}{\beta} \varphi_\alpha \varphi_\beta ds\,.\]

Á hægri hliðinni höfum við

\[\begin{split}&&\langle f, \varphi_\beta\rangle= \int_S f\varphi_\beta dA \\ && \int_{\partial S_2} p\frac{\gamma}{\beta} \varphi_\beta ds\,.\end{split}\]

Á fylkjaformi \(A{\mathbf c}={\mathbf b}\) er

\[\begin{split}&& a_{\beta, \alpha}= \int_S \left(p \nabla \varphi_\alpha \cdot \nabla \varphi_\beta +q \varphi_\alpha \varphi_\beta\right) dA+\int_{\partial S_2} p\frac{\alpha}{\beta} \varphi_\alpha \varphi_\beta ds, \\ && b_\beta = \int_S f\varphi_\beta dA+\int_{\partial S_2} p\frac{\gamma}{\beta} \varphi_\beta ds- \sum_{\alpha\in Q} {\gamma_\alpha\over \alpha_\alpha} \left(\int_S \left(p \nabla \varphi_\alpha \cdot \nabla \varphi_\beta +q \varphi_\alpha \varphi_\beta\right) dA+\int_{\partial S_2}p\frac{\alpha}{\beta} \varphi_\alpha \varphi_\beta ds\right)\,.\end{split}\]

Nú þurfum við að reikna út heildin að ofan. Við nálgum þau með því að nota reglu „miðpunktanna“, það þýðir að fyrir sérhvert samfellt fall \(\psi\) nálgum við heildi yfir þríyrning \(T_{A,B,C}\) á eftirfarandi hátt

\[\int_{T_{A,B,C}} \psi(x,y)dA\approx \psi\left(\tfrac{x_A+x_B+x_C}{3},\tfrac{y_A+y_B+y_C}{3}\right) area(T_{A,B,C}) ={|d|\over 2}\psi(M_{A,B,C})\,\]

þar sem \(M_{A,B,C}\) er massmiðja þríhyrningsins \(T_{A,B,C}\).

Við skoðum ýmsa liði.

1. Í \(b_\beta\) höfum við

\[\int_S f\varphi_\beta dA\approx \sum_{T_{\beta}}f(M_{(\beta)}){|d|\over 6},\]

af því að \(\varphi_\beta(M_{(\beta)})=\tfrac 13\). Athugum að summan hér þýðir að við þurfum að summa bara yfir þríhyrninga sem hafa punkt \(\beta\) fyrir hornpunkt (munið skilgreinguna á þúfugrunnföllum).

2. Í \(b_\beta\) og í \(a_{\beta \alpha}\) höfum við

\[\int_S p \nabla \varphi_\alpha \cdot \nabla \varphi_\beta dA \approx \sum_{T_{\beta}} p(M_{(\beta)}){{\mathbf l}_\alpha^R\cdot {\mathbf l}_\beta^R\over 2|d|}=\sum_{T_{\beta}} p(M_{(\beta)}){{\mathbf l}_\alpha\cdot {\mathbf l}_\beta\over 2|d|},\]

þar sem summan er yfir þríhyrninga sem hafa punkt \(\beta\) fyrir hornpunkt. Munið að innfeldi \(\nabla \varphi_\alpha \cdot \nabla \varphi_\beta\) er ekki núll aðeins ef \(\alpha\) og \(\beta\) eru tveir hornpunktar \(T_{\beta}\).

3. Í \(b_\beta\) og í \(a_{\beta \alpha}\) höfum við

\[\int_S q \varphi_\alpha \varphi_\beta dA \approx \sum_{T_{\beta}} q(M_{(\beta)}){|d|\over 18},\]

af því að \(\varphi_\beta(M_{(\beta)})=\tfrac 13\). Aftur, við summun yfir þríhyrninga sem hafa punkt \(\beta\) fyrir hornpunkt.

Athugið

Í kennslubókinni er heildið að ofan nálgað á eftirfarandi hátt

\[\int_{T_{A,B,C}} \psi(x,y)\, dA \approx \tfrac{|d|}{6}\big(\psi_{A,B}+\psi_{B,C}+\psi_{C,A}\big),\]

þar sem \(\psi\) er samfellt fall, \(\psi_{A,B}, \psi_{B,C}\) og \(\psi_{C,A}\) tákna gildi fallsins \(\psi\) í miðpunktum hliðanna \(AB, BC\) og \(CA\).

Af 2. og 3. leiðir að

\[\int_S \left(p \nabla \varphi_\alpha \cdot \nabla \varphi_\beta + q \varphi_\alpha \varphi_\beta\right) dA \approx \sum_{T_{\beta}}\left(p(M_{(\beta)}){{\mathbf l}_\alpha\cdot {\mathbf l}_\beta\over 2|d|}+q(M_{(\beta)}){|d|\over 18}\right).\]

Athugið

Í kennslubókinni er heildið að ofan nálgað á eftirfarandi hátt

\[\begin{split}\int_{S}\big(p\nabla \varphi_\alpha\cdot \nabla \varphi_\beta +q\varphi_\alpha\varphi_\beta\big)\, dA \approx \sum_{T_{\beta}}\dfrac {p(M_{(\beta)})}{2 |d|}{{\mathbf l}_\alpha\cdot {\mathbf l}_\beta} +\sum_{T_{\beta}}\begin{cases} \tfrac 1{12} q(M_{(\beta)})\, |d|,& \alpha=\beta,\\ \tfrac 1{24} q(M_{(\beta)})\, |d|,& \alpha\neq \beta. \end{cases}\end{split}\]

4. Í síðasta skrefi þurfum við að nálga jaðarheildin yfir \(\partial S_2\) í veiku framsetningunni. Við notum reglu Simpsons, sem segir að

\[\int_a^b f(t)\, dt\approx \tfrac 16\big(f(a)+4f(\tfrac 12(a+b))+f(b)\big)(b-a)\]

Við táknum opna línustrikið sem liggur í \(\partial S_2\) milli punkta \(A\) og \(B\) með \(S_{A,B}\), lengd þess með \(|S_{A,B}|\), og miðpunkt þess með \(m_{A,B}\).

Athugum að

\[\varphi_A(m_{A,B})=\varphi_B(m_{A,B})=\tfrac 12\qquad \varphi_C(m_{A,B})=0.\]

Þá fáum við

\[\begin{split}\begin{gathered} \int_{S_{A,B}} \psi\, \varphi_\alpha^2\, ds \approx \tfrac 16\big(\psi(x_\alpha,y_\alpha)+ \psi(m_{A,B})\big) |S_{A,B}|, \qquad \alpha=A,B, \\ \int_{S_{A,B}} \psi\, \varphi_A\varphi_B\, ds \approx \tfrac 16 \psi(m_{A,B}) |S_{A,B}|, \\ \int_{S_{A,B}} \psi \, \varphi_\alpha\, ds \approx \tfrac 16\big(\psi(x_\alpha,y_\alpha)+2\psi(m_{A,B})\big) |S_{A,B}| \qquad \alpha=A,B.\end{gathered}\end{split}\]

Að lokum fáum við fyrir jaðarheildin

\[\begin{gathered} \int_{S_{A,B}}\dfrac{p \alpha}{\beta} \varphi_\alpha^2\, ds \approx \dfrac 16\bigg( p(x_\alpha,y_\alpha) \dfrac{\alpha(x_\alpha,y_\alpha)} {\beta(x_\alpha,y_\alpha)} +p(m_{A,B}) \dfrac{\alpha(x_A,y_A)+\alpha(x_B,y_B)} {\beta(x_A,y_A)+\beta(x_B,y_B)} \bigg) |S_{A,B}|, \quad \alpha=A,B. \end{gathered}\]

\[\int_{S_{A,B}}\dfrac{p \alpha}{ \beta} \varphi_A\varphi_B\, ds \approx \frac 16 p(m_{A,B}) \dfrac{\alpha(x_A,y_A)+\alpha(x_B,y_B)} {\beta(x_A,y_A)+\beta(x_B,y_B)} |S_{A,B}|.\]

\[\int_{S_{A,B}}\dfrac{p \gamma}{\beta} \varphi_\alpha\, ds \approx \dfrac 16\bigg( p(x_\alpha,y_\alpha) \dfrac{\gamma(x_\alpha,y_\alpha)} {\beta(x_\alpha,y_\alpha)} +2 p(m_{A,B}) \dfrac{\gamma(x_A,y_A)+\gamma(x_B,y_B)} {\beta(x_A,y_A)+\beta(x_B,y_B)} \bigg) |S_{A,B}|, \quad j=A,B.\]

Til þess að reikna út jaðarheildi yfir \(\partial S_2\) þurfum við að summa yfir öll línustrikin sem liggja í \(\partial S_2\).